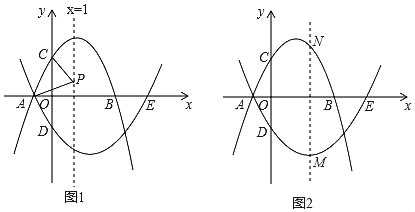
题目内容
【题目】(1)如图1是一个重要公式的几何解释.请你写出这个公式: ;
(2)如图2,已知![]() ,
,![]() ,且
,且![]() 三点共线.
三点共线.
试证明![]() ;
;

(3)勾股定理是几何学中的明珠,千百年来,人们对它的证明趋之若骛,有资料表明,关于勾股定理的证明方法已有500余种.课本中介绍了比较有代表性的赵爽弦图.
伽菲尔德(Garfield,1881年任美国第20届总统)利用图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),请你写出该证明过程.
【答案】⑴ ![]() .⑵见解析;⑶见解析;
.⑵见解析;⑶见解析;
【解析】
(1)由大正方形面积的两种计算方法即可得出结果;
(2)由全等三角形的性质得出∠BAC=∠DCE,再由角的互余关系得出∠ACB+∠DCE=90°,即可得出结论;
(3)梯形ABDE的面积用两种计算方法即可得出结论.
⑴ 这个公式为![]() .
.
⑵ ∵![]() ,∴
,∴![]() .
.
![]() .
.
由于点![]() 共线,
共线,
所以![]() .
.
⑶ 梯形![]() 的面积为
的面积为
![]() ;
;
另一方面,梯形![]() 可分成三个直角三角形,其面积又可以表示成
可分成三个直角三角形,其面积又可以表示成![]()
∴![]() ,即
,即![]()

练习册系列答案
相关题目