题目内容
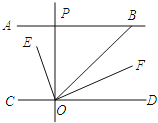
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A﹙-2,-5﹚、C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图象交于点A﹙-2,-5﹚、C﹙5,n﹚,交y轴于点B,交x轴于点D.
(1)求反比例函数y=![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA、OC,求△AOC的面积;
(3)写出使一次函数的值大于反比例函数的x的取值范围.

【答案】(1)y=![]() ;y=x﹣3;(2)10.5;(3)﹣2<x<0或x>5;
;y=x﹣3;(2)10.5;(3)﹣2<x<0或x>5;
【解析】
(1)把A(﹣2,﹣5)代入y=![]() 求得m的值,然后求得C的坐标,利用待定系数法求得直线的解析式即可;(2)先求得OB的长,再根据S△AOC=S△AOB+S△BOC即可求得△AOC的面积;(3)根据图象和交点坐标即可求得.
求得m的值,然后求得C的坐标,利用待定系数法求得直线的解析式即可;(2)先求得OB的长,再根据S△AOC=S△AOB+S△BOC即可求得△AOC的面积;(3)根据图象和交点坐标即可求得.
(1)把点A(﹣2,﹣5)代入反比例函数的解析式y=![]() 得:﹣5=
得:﹣5=![]() ,
,
解得:m=10,
即反比例函数的解析式为:y=![]() ,
,
把点C(5,n)代入解析式y=![]() 得:n=2,
得:n=2,
即点C的坐标为(5,2),
把点A(﹣2,﹣5)和点C(5,2)代入y=kx+b得:
![]() ,
,
解得:![]() ,
,
即一次函数的表达式为y=x﹣3,
(2)把x=0代入y=x﹣3得:y=﹣3,
即OB=3,
∵C(5,2),A﹙-2,-5﹚,
∴S△AOC=S△AOB+S△BOC=![]() OB|2|+
OB|2|+![]() OB5=
OB5=![]() OB(2+5)=10.5.
OB(2+5)=10.5.
(3)通过观察图象可知:
使一次函数的值大于反比例函数的x的取值范围为:﹣2<x<0或x>5.

 阅读快车系列答案
阅读快车系列答案【题目】某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
项目类型 | 频数 | 频率 |
跳长绳 | 25 | a |
踢毽子 | 20 | 0.2 |
背夹球 | b | 0.4 |
拔河 | 15 | 0.15 |
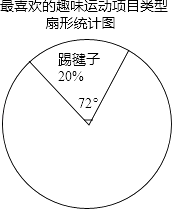
(1)直接写出a= , b=;
(2)利用频数分布表中的数据,在图中绘制扇形统计图(注明项目、百分比、圆心角);
(3)若全校共有学生1200名,估计该校最喜爱背夹球和拔河的学生大约有多少人?