题目内容
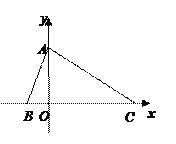
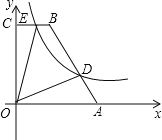
【题目】如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0), (2,6),点D为AB上一点,且BD=2AD,双曲线y=![]() (k>0)经过点D,交BC于点E.
(k>0)经过点D,交BC于点E.
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
【答案】(1)y=![]() ;(2)12.
;(2)12.
【解析】(1)作BM⊥x轴于M,作BN⊥x轴于N,利用点A,B的坐标得到BC=OM=5,BM=OC=6,AM=3,再证明△ADN∽△ABM,利用相似比可计算出DN=2,AN=1,则ON=OA﹣AN=4,得到D点坐标为(4,2),然后把D点坐标代入y=![]() 中求出k的值即可得到反比例函数解析式;
中求出k的值即可得到反比例函数解析式;
(2)根据反比例函数k的几何意义和S四边形ODBE=S梯形OABC﹣S△OCE﹣S△OAD进行计算.
解:(1)作BM⊥x轴于M,作DN⊥x轴于N,如图,

∵点A,B的坐标分别为(5,0),(2,6),
∴BC=OM=2,BM=OC=6,AM=3,
∵DN∥BM,
∴△ADN∽△ABM,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴DN=2,AN=1,
∴ON=OA﹣AN=4,
∴D点坐标为(4,2),
把D(4,2)代入y=![]() 得k=2×4=8,
得k=2×4=8,
∴反比例函数解析式为y=![]() ;
;
(2)S四边形ODBE=S梯形OABC﹣S△OCE﹣S△OAD
=![]() ×(2+5)×6﹣
×(2+5)×6﹣![]() ×|8|﹣
×|8|﹣![]() ×5×2
×5×2
=12.
“点睛”本题考查了反比例函数综合题:熟练掌握反比例函数图象上点的坐标特征、反比例函数k的几何意义和梯形的性质;理解坐标与图形的性质;会运用相似比计算线段的长度.

练习册系列答案
相关题目