题目内容
【题目】点C,点D是线段AB上任意两点.
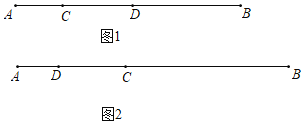
(1)如图1,若点D是线段BC的中点,AD=18,AC=6,求线段BD的长;
(2)如图2,若点C把线段AB分为2:3的两段(AC<BC),点D分线段AB为1:5两段(AD<BD),DC=7,求线段AB的长.
【答案】(1)12;(2)30.
【解析】
(1)先根据线段的和差求出线段CD,再根据线段中点的定义即可解答;
(2)根据题意得出:点D分线段AB为1:5两段(AD<BD),设AD=x,则BD=5x,进而得出AB=6x,再根据点C把线段AB分为2:3的两段可得AC=![]() ,然后用含有x的代数式表示出CD,即可得出答案.
,然后用含有x的代数式表示出CD,即可得出答案.
解:(1)∵AD=18,AC=6,
∴CD=AD﹣AC=12,
又∵点D是线段BC的中点,
∴BD=CD=12;
(2)根据题意可设AD=x,则BD=5x,
∴AB=6x,
∵点C把线段AB分为2:3的两段,
∴AC=![]() ,
,
∴CD=AC﹣AD=![]() ,
,
∵CD=7,
∴![]() ,
,
解得x=5.
∴AB=6x=30.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目