题目内容
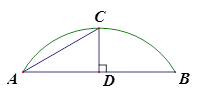
在Rt△ACB中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.

(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD∶AO=8∶5,BC=3,求BD的长.

(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD∶AO=8∶5,BC=3,求BD的长.
(1)见解析;(2)BD= .
.
 .
.试题分析:(1)要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可;
(2)通过作辅助线,根据已知条件求出∠CBD的度数,在Rt△BCD中求解即可.
试题解析:
(1)直线BD与⊙O的位置关系是相切.
证明:连结OD,DE.
∵∠C=90°,
∴∠CBD+∠CDB=90°.
∵∠A=∠CBD,
∴∠A+∠CDB=90°.
∵OD=OA,
∴∠A=∠ADO.
∴∠ADO+∠CDB=90°.
∴∠ODB=180°-90°=90°.
∴OD⊥BD.
∵OD为半径,
∴BD是⊙O切线.

(2)∵AD:AO=8:5,
∴
 =
= .
.∴由勾股定理得AD:DE:AE=8:6:10.
∵∠C=90°,∠CBD=∠A.
∴△BCD∽△ADE.
∴DC:BC:BD=DE:AD:AE=6:8:10.
∵BC=3,
∴BD=
 .
.
练习册系列答案
相关题目
 、
、 、
、 、
、 是圆上的点,
是圆上的点, 则
则 度.
度.
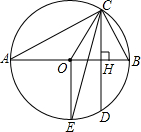
 的中点,连接0E,CE.求证:CE平分∠OCD.
的中点,连接0E,CE.求证:CE平分∠OCD.


 米,∠CAD=30°,请你帮助文物学家完成下面两项工作:
米,∠CAD=30°,请你帮助文物学家完成下面两项工作: