题目内容
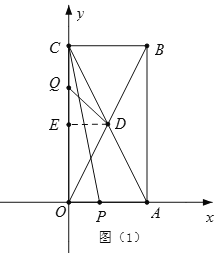
【题目】如图1所示在平面直角坐标系中,有长方形OABC,O是坐标原点,A(a,0),C(0,b),且a,b满足![]()
(1)求A,B,C三点坐标;
(2)如图2所示,长方形对角线OB、AC交于D点,若有一点P从A点出发,以1单位/秒速度向x轴负方向匀速运动,同时另一点Q从O出发,以2个单位/秒,沿长方形边长O-C-B顺时针匀速运动,当Q到达B点时P、Q同时停止运动,设P点开始运动时间为t,请问:当t为何值时有S△OCP≤S△ODQ ?

【答案】(1)A(4,0)B(4,8)C(0,8);(2)![]() ≤t<4或4<t≤5.
≤t<4或4<t≤5.
【解析】
(1)由算术平方根的被开方数为非负数可求得a的值,继而求得b的值,再根据长方形的性质即可求得答案;
(2)分0≤t<4,t=4,4<t≤6三种情况分别讨论即可求得答案.
(1)由![]() ,得
,得
![]() ,
,
解得a=4,
所以b-2=6,
解得b=8,
所以A(4,0),C(0,8),
所以OA=4,OC=8,
又因为ABCD是长方形,
所以AB=OC=8,BC=OA=4,
所以C(4,8);
(2)过D作DE⊥OC于点E,则有DE=2,OE=CE=4,
①当0≤t<4时,如图(1),
S△OCP=![]() OC·OP=
OC·OP=![]() ×8×(4-t),
×8×(4-t),
S△ODQ=![]() OQ·DE=
OQ·DE=![]() ×2t×2,
×2t×2,
令S△OCP≤S△ODQ,
即有![]() ×8×(4-t)≤
×8×(4-t)≤![]() ×2t×2,
×2t×2,
解得t≥![]() ;
;
②当t=4时,△OPC不存在,舍去;
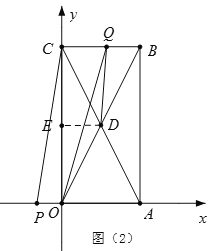
③当4<t≤6时,如图(2)
S△OCP=![]() OC·OP=
OC·OP=![]() ×8×(t-4),
×8×(t-4),
S△ODQ=S△OBC-S△OCQ-S△DBQ=![]() OC·BC-
OC·BC-![]() OC·CQ-
OC·CQ-![]() BQ·CE
BQ·CE
=![]() ×4×8-
×4×8-![]() ×8×(2t-8)-
×8×(2t-8)-![]() ×(8+4-2t)×4,
×(8+4-2t)×4,
令S△OCP≤S△ODQ,
即有![]() ×8×(t-4)≤
×8×(t-4)≤![]() ×4×8-
×4×8-![]() ×8×(2t-8)-
×8×(2t-8)-![]() ×(8+4-2t)×4,
×(8+4-2t)×4,
解得 t≤5,
综上所述,当![]() ≤t<4或4<t≤5时成立.
≤t<4或4<t≤5时成立.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案