题目内容
【题目】如图，在△ABC中∠BAC=90°,AB=AC=2
,圆A的半径1，点O在BC边上运动（与点B/C不重合），设BO=X,△AOC的面积是y.
⑴求y关于x的函数关系式及自变量的取值范围；
⑵以点O位圆心，BO为半径作圆O，求当○O与○A相切时，△AOC的面积.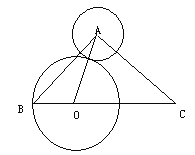
【答案】（1）过点A作AH⊥BC于H
∵∠BAC=90°，AB=AC=
∴BC=4，AH=2，
∴
即y＝－x＋4（0<x<4）
（2）当点O与点H重合时，圆O与圆A相交，不合题意；当点O与点H不重合时，在Rt△AOH中，
∵圆A的半径为1，圆O的半径为x，
∴①当圆A与圆O外切时，
解得x＝
，
＝y＝
②当圆A与圆O内切时，
解得x＝
，＝y＝
【解析】
（1）由∠BAC=90°，AB="AC=2"
，根据勾股定理即可求得BC，且∠B=∠C，然后作AM⊥BC，由S△AOC=
OCAM，即可求得y关于x的函数解析式；
（2）由⊙O与⊙A外切或内切，即可求得ON的值，继而求得△AOC的面积．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
