Question

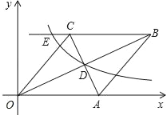
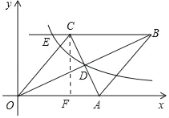
【题目】如图，在直角坐标系中有菱形OABC，A点的坐标为（10，0），对角线OB、AC相交于点D，双曲线y＝（x＞0）经过点D，交BC的延长线于点E，且OBAC＝160，则点E的坐标为_____．

Answer 1

【答案】（4，8）．

【解析】

过点C作CF⊥x轴于点F，由A点坐标可得菱形的边长，利用菱形面积可求出CF的长，由勾股定理可求出OF的长，即可得出C点坐标，进而可求出AC中点D的坐标，代入双曲线解析式可得k的值，根据CF的长可得E点纵坐标，代入双曲线解析式即可求出E点的横坐标，即可得答案.

过点C作CF⊥x轴于点F，

∵OBAC＝160，A点的坐标为（10，0），

∴S菱形OABC=OACF＝OBAC＝×160＝80，菱形OABC的边长为10，

∴CF＝8，

在Rt△OCF中，

∵OC＝10，CF＝8，

∴OF＝＝＝6，

∴C（6，8），

∵点D是线段AC的中点，

∴D点坐标为（，），即（8，4），

∵双曲线y＝（x＞0）经过D点，

∴4＝，即k＝32，

∴双曲线的解析式为：y＝（x＞0），

∵CF＝8，BE//x轴，

∴E点纵坐标为8，

把y=8代入y＝（x＞0）得：8=，

解得：x=4，

∴E点坐标为（4，8），

故答案为（4，8）．