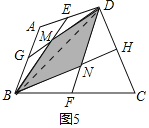
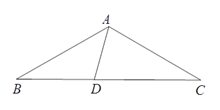МвДҝДЪИЭ
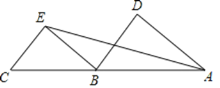
ЎҫМвДҝЎҝОКМвҪвҫцЈәИзНј1Ј¬![]() ЦРЈ¬
ЦРЈ¬![]() ОӘ
ОӘ![]() ұЯЙПөДЦРПЯЈ¬Фт
ұЯЙПөДЦРПЯЈ¬Фт![]() ______
______![]() .
.
ОКМвМҪҫҝЈә
ЈЁ1Ј©ИзНј2Ј¬![]() ·ЦұрКЗ
·ЦұрКЗ![]() өДЦРПЯЈ¬
өДЦРПЯЈ¬![]() Ул
Ул![]() ПаөИВрЈҝ
ПаөИВрЈҝ
ҪвЈә![]() ЦРЈ¬УЙОКМвҪвҫцөДҪбВЫҝЙөГЈ¬
ЦРЈ¬УЙОКМвҪвҫцөДҪбВЫҝЙөГЈ¬![]() Ј¬
Ј¬![]() .
.
Ўа![]()
Ўа![]()
јҙ![]() .
.
ЈЁ2Ј©Нј2ЦРЈ¬·ВХХЈЁ1Ј©өД·Ҫ·ЁЈ¬КФЛөГч![]() .
.
ЈЁ3Ј©ИзНј3Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ·ЦұрКЗ
·ЦұрКЗ![]() өДЦРПЯЈ¬Фт
өДЦРПЯЈ¬Фт![]() ______
______![]() Ј¬
Ј¬![]() ______
______![]() Ј¬
Ј¬![]() ______
______![]() .
.

ОКМвНШХ№Јә
ЈЁ1Ј©ИзНј4Ј¬![]() ·ЦұрОӘЛДұЯРО
·ЦұрОӘЛДұЯРО![]() өДұЯ
өДұЯ![]() өДЦРөгЈ¬ЗлЦұҪУРҙіцТхУ°Іҝ·ЦөДГж»эУлЛДұЯРО
өДЦРөгЈ¬ЗлЦұҪУРҙіцТхУ°Іҝ·ЦөДГж»эУлЛДұЯРО![]() өДГж»эЦ®јдөДКэБҝ№ШПөЈә
өДГж»эЦ®јдөДКэБҝ№ШПөЈә![]() ______
______![]() .
.

ЈЁ2Ј©ИзНј5Ј¬![]() ·ЦұрОӘЛДұЯРО
·ЦұрОӘЛДұЯРО![]() өДұЯ
өДұЯ![]() өДЦРөгЈ»ЗлЦұҪУРҙіцТхУ°Іҝ·ЦөДГж»эУлЛДұЯРО
өДЦРөгЈ»ЗлЦұҪУРҙіцТхУ°Іҝ·ЦөДГж»эУлЛДұЯРО![]() өДГж»эЦ®јдөДКэБҝ№ШПөЈә
өДГж»эЦ®јдөДКэБҝ№ШПөЈә![]() ______
______![]() .
.
Ўҫҙр°ёЎҝОКМвҪвҫцЈәЈЁ1Ј©![]() ЈЁ2Ј©јыҪвОцЈ»ЈЁ3Ј©
ЈЁ2Ј©јыҪвОцЈ»ЈЁ3Ј©![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј»
Ј»
ОКМвНШХ№ЈәЈЁ1Ј©![]() Ј»ЈЁ2Ј©
Ј»ЈЁ2Ј©![]() Ј»
Ј»
ЎҫҪвОцЎҝ
ОКМвҪвҫцЈәЈЁ1Ј©ёщҫЭЦРПЯЖҪ·ҪГж»эјҙҝЙЗуҪвЈ»
ЈЁ2Ј©ёщҫЭ![]() Ј¬·ЦұрјхИҘЎчBOCөДГж»эјҙҝЙЗуҪвЈ»
Ј¬·ЦұрјхИҘЎчBOCөДГж»эјҙҝЙЗуҪвЈ»
ЈЁ3Ј©ёщҫЭЦРПЯөДРФЦКөГөҪёчРЎИэҪЗРОөДГж»э¶јПаөИЈ¬јҙҝЙЗуҪвЈ»
ОКМвНШХ№ЈәЈЁ1Ј©Б¬ҪУBDЈ¬ёщҫЭОКМвҪвҫцЈЁ1Ј©өДҪбВЫјҙҝЙЗуҪвЈ»
ЈЁ2Ј©Б¬ҪУBDЈ¬ёщҫЭОКМвҪвҫцЈЁ2Ј©өДҪбВЫјҙҝЙЗуҪв.
ОКМвҪвҫцЈәЈЁ1Ј©ЎЯ![]() ЦРЈ¬
ЦРЈ¬![]() ОӘ
ОӘ![]() ұЯЙПөДЦРПЯЈ¬
ұЯЙПөДЦРПЯЈ¬
Ўа![]()
![]()
![]() .
.
ЈЁ2Ј©ҪвЈә![]() ЦРЈ¬УЙОКМвҪвҫцөДҪбВЫҝЙөГЈ¬
ЦРЈ¬УЙОКМвҪвҫцөДҪбВЫҝЙөГЈ¬![]() Ј¬
Ј¬![]() .
.
Ўа![]()
Ўа![]()
јҙ![]() .
.
ЈЁ3Ј©ЎЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ·ЦұрКЗ
·ЦұрКЗ![]() өДЦРПЯЈ¬
өДЦРПЯЈ¬
УЙЈЁ2Ј©ҝЙөГ![]()
Ўа![]()
![]()
![]() Ј¬
Ј¬![]()
![]()
![]() Ј¬
Ј¬![]()
![]()
![]() .
.
ОКМвНШХ№ЈәЈЁ1Ј©ИзНјЈ¬Б¬ҪУBDЈ¬УЙОКМвҪвҫцЈЁ1Ј©өДҪбВЫөГ![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,
Ўа![]()
![]()
![]()
![]()
![]()

ЈЁ2Ј©ИзНјБ¬ҪУBDЈ¬ёщҫЭОКМвҪвҫцЈЁ2Ј©өДҪбВЫөГ
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,
Ўа![]()
![]()
![]()
![]()
![]()

 ГыРЈҝОМГПөБРҙр°ё
ГыРЈҝОМГПөБРҙр°ёЎҫМвДҝЎҝДіЦРС§ОӘБЛҪвҫЕДкј¶С§ЙъөДЙнМеЛШЦКЗйҝцЈ¬Лж»ъійІйБЛҫЕДкј¶Іҝ·ЦС§ЙъТ»·ЦЦУМшЙюҙОКэЈ¬»жЦЖіЙИзПВНіјЖНјұнЈЁНј1Ј¬Нј2Ј¬ұнЈ©Ј®
өИј¶ | Т»·ЦЦУМшЙюҙОКэx | ИЛКэ |
A | xЈҫ180 | 12 |
B | 150ЈјxЎЬ180 | 14 |
C | 120ЈјxЎЬ150 | a |
D | xЎЬ120 | b |

ЗлҪбәПНјұнНкіЙПВБРОКМвЈә
ЈЁ1Ј©ұн1ЦРa=ЎЎ ЎЎЈ¬b=ЎЎ ЎЎЈ»
ЈЁ2Ј©Зл°СНј1әННј2І№ідНкХыЈ»
ЈЁ3Ј©ТСЦӘёГРЈУР1000ГыҫЕДкј¶С§ЙъЈ¬ИфФЪТ»·ЦЦУДЪМшЙюҙОКэІ»ҙуУЪ120ҙОөДОӘІ»әПёсЈ¬ФтёГРЈҫЕДкј¶С§ЙъТ»·ЦЦУМшЙюІ»әПёсөДС§Йъ№АјЖОӘЎЎ ЎЎИЛЈ®