题目内容
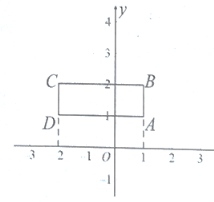
【题目】如图，已知△ABC的三个顶点分别为A（2，3）、B（3，1）、C（－2，－2）．
（1）请在图中作出△ABC关于y轴的轴对称图形△DEF（A、B、C的对应点分别是D、E、F），并直写出D、E、F的坐标．
（2）求四边形ABED的面积．
【答案】（1）图见解析；D(-2,3)，E(-3,1)，F(2,-2) （2）10
【解析】
（1）首先确定A、B、C的关于y轴的对称点D、E、F的位置，再顺次连接即可，然后写出D、E、F的坐标；
（2）根据梯形的面积公式，即可求解．
（1）如图所示：△DEF即为所求三角形，由图形可知：D(-2，3)，E(-3，1)，F(2，-2)；
（2）连接AD，BE，
∵AD∥BE，
∴四边形ABED是梯形，
∴四边形ABED的面积=
．
【题目】从2开始，连续的偶数相加，它们和的情况如下表：
加数的个数n | S |
1 | 2=1×2 |
2 | 2＋4=6=2×3 |
3 | 2＋4＋6=12=3×4 |
4 | 2＋4＋6＋8=20=4×5 |
5 | 2＋4＋6＋8＋10=30=5×6 |
（1）若n=8时，则S的值为_____________．
（2）根据表中的规律猜想：用n的式子表示S的公式为：S=2+4+6+8+…+2n=__________________．
（3）根据上题的规律计算2+4+6+8+10+…+98+100
的值．
【题目】如果一个多边形的各边都相等且各角也都相等，那么这样的多边形叫做正多边形，如正三角形就是等边三角形，正四边形就是正方形，如下图，就是一组正多边形，
(1)观察上面每个正多边形中的∠α，填写下表：
正多边形边数 | 3 | 4 | 5 | 6 | …… | n |
∠α的度数 | ______° | _____° | ______° | ______° | …… | _____° |
(2)根据规律，计算正八边形中的∠α的度数.
(3)是否存在正n边形使得∠α=21°？若存在，请求出n的值，若不存在，请说明理由.
【题目】问题：探究函数的图象与性质．
小华根据学习函数的经验，对函数的图象与性质进行了探究．下面是小华的探究过程，请补充完整：
在函数
中，自变量
可以是任意实数；
（1）下表是
与的几组对应值．
| … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| … | 1 | 0 | -1 | -2 | -1 | 0 |
| … |
①
______；
②若
，
为该函数图象上不同的两点，则
______；
（2）如图，在平面直角坐标系
中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；
（3）根据函数图象可得函数的性质：
①该函数的最小值为______；
②再写出该函数一条性质____________．
