Question

【题目】四边形ABCD内接于⊙O，点E为AD上一点，连接AC，CB，∠B=∠AEC．

（1）如图1，求证：CE=CD；

（2）如图2，若∠B+∠CAE=120°，∠ACD=2∠BAC，求∠BAD的度数；

（3）如图3，在（2）的条件下，延长CE交⊙O于点G，若tan∠BAC= ，EG=2，求AE的长．

【答案】（1）见解析；（2）60°；（3）7.

【解析】试题分析：(1)利用圆的内接四边形定理得到∠CED=∠CDE.

(2) 作CH⊥DE于H, 设∠ECH=α，由（1）CE=CD，用α表示∠CAE，∠BAC，而∠BAD=∠BAC+∠CAE.（3）连接AG，作GN⊥AC，AM⊥EG，先证明∠CAG=∠BAC，设NG=5m，可得AN=11m，利用直角AGM, AEM，勾股定理可以算出m的值并求出AE长.

试题解析：

（1）解：证明：∵四边形ABCD内接于⊙O.

∴∠B+∠D=180°，

∵∠B=∠AEC，

∴∠AEC+∠D=180°，

∵∠AEC+∠CED=180°，

∴∠D=∠CED，

∴CE=CD．

（2）解：作CH⊥DE于H．

设∠ECH=α，由（1）CE=CD，

∴∠ECD=2α，

∵∠B=∠AEC，∠B+∠CAE=120°，

∴∠CAE+∠AEC=120°，

∴∠ACE=180°﹣∠AEC﹣∠ACE=60°，

∴∠CAE=90°﹣∠ACH=90°﹣（60°+α）=30°﹣α，

∠ACD=∠ACH+∠HCD=60°+2α，

∵∠ACD=2∠BAC，

∴∠BAC=30°+α，

∴∠BAD=∠BAC+∠CAE=30°+α+30°﹣α=60°．

（3）解：连接AG，作GN⊥AC，AM⊥EG，

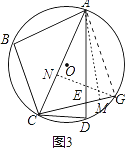
∵∠CED=∠AEG，∠CDE=∠AGE，∠CED=∠CDE，

∴∠AEG=∠AGE，

∴AE=AG，

∴EM=MG=EG=1，

∴∠EAG=∠ECD=2α，

∴∠CAG=∠CAD+∠DAG=30°﹣α+2α=∠BAC，

∵tan∠BAC=，

∴设NG=5m，可得AN=11m，AG==14m，

∵∠ACG=60°，

∴CN=5m，AM=8m，MG==2m=1，

∴m=，

∴CE=CD=CG﹣EG=10m﹣2=3，

∴AE===7．

【题型】解答题
【结束】
27

【题目】二次函数y=（x﹣1）2+k分别与x轴、y轴交于A、B、C三点，点A在点B的左侧，直线y=﹣x+2经过点B，且与y轴交于点D．

（1）如图1，求k的值；

（2）如图2，在第一象限的抛物线上有一动点P，连接AP，过P作PE⊥x轴于点E，过E作EF⊥AP于点F，过点D作平行于x轴的直线分别与直线FE、PE交于点G、H，设点P的横坐标为t，线段GH的长为d，求d与t的函数关系式，并直接写出t的取值范围；

（3）在（2）的条件下，过点G作平行于y轴的直线分别交AP、x轴和抛物线于点M、T和N，tan∠MEA= ，点K为第四象限抛物线上一点，且在对称轴左侧，连接KA，在射线KA上取一点R，连接RM，过点K作KQ⊥AK交PE的延长线于Q，连接AQ、HK，若∠RAE﹣∠RMA=45°，△AKQ与△HKQ的面积相等，求点R的坐标．

Answer 1

【答案】（1）﹣4；（2）d=2t﹣6（t＞3）；（3）（﹣， ）．

【解析】试题分析：（1）利用一次函数求出B点坐标，代入二次函数可求二次函数解析式.

(2) 先证明四边形DOEH为矩形，利用=，代入数值求出d和t的关系.

(3) 先证明GHET为矩形，则，得到t的值，作HW⊥KQ，

证明四边形AKWH是矩形，接着证明△RAM≌△HAN，待定系数法证明直线MR的解析式为y直线AK的解析式，△AKQ与△HKQ的面积相等，求点R的坐标

试题解析：

（1）解：在一次函数y=﹣x+2中，令y=0，得：0=﹣x+2，

解得x=3，

∴B（3，0），

令x=0得y=2，

∴D（0，2），

将B（3，0），代入y=（x﹣1）2+k得：4+k=0，

∴k=﹣4．

（2）解：如答图1所示：

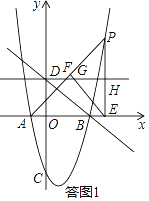
∵PE⊥x轴，EF⊥AP，

∴∠PEA=∠EFA=90°，

∵∠PEF+∠FEA=90°，∠PAE+∠FEA=90°，

∴∠PEF=∠PAE，

∵DH∥x轴 HE⊥x轴,

∴∠HDO=∠DOE=∠PEO=90°,

∴四边形DOEH为矩形，

∴HE=2，

∴=，

∴，

∴d=2t﹣6．（t＞3）．

（3）解：∵∠TGH=∠GTE=∠TEH=90°，

∴GHET为矩形，

∴GH=d=ET=2t﹣6，

∵tan∠MEB=，

∴，

∴MT=3t﹣9，

∵，/span>

∴，

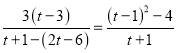解得t=4．

∴P（4，5）．

∴AT=AE﹣ET=t+1﹣（2t﹣6）=7﹣t=3，

∴M（2，3），

把x=2代入y=x2﹣2x﹣3中，得N（2，﹣3），

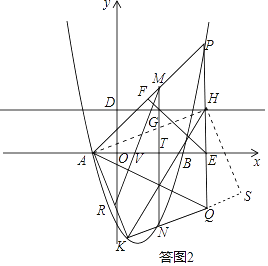
∴MT=TN=AT，∠MAT=90°．

∵∠RAE﹣∠RMA=45°，

∴∠RAE﹣45°=∠RMA，

∴∠RAM=∠RMA，

∵S△AKQ=S△HKQ ， 作HW⊥KQ，

∴AK∥HW，AK=HW，

∴四边形AKWH是矩形，

∴∠RAH=∠HAK=90°，

∴∠RAM=∠HAN．

∵A（﹣1，0），H（4，2），N（2，﹣3），

∴AH=HN=，

∴∠HAN=∠HNA=∠RAM=∠RMA．

又∵AM=AN，

∴△RAM≌△HAN，

∴AR=AH，

过R作RL⊥x轴，

∴∠RLA=∠AEH=90°，

∵∠RAL+∠HAE=90，∠HAE+∠AHE=90，

∴∠RAL=∠AHE，

∴△ARL≌△AHE，

∴RL=AE=5，AL=HE=3，

由∠RAM﹣∠RMA=45°可知∠RAV=∠RVA，∠RMT=∠HAE，tan∠RMT=tan∠HAE=，

V（，0），

直线MR的解析式为y= x﹣2，直线AK的解析式为y=﹣x﹣，

交点R（﹣， ）．