��Ŀ����
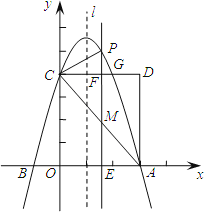
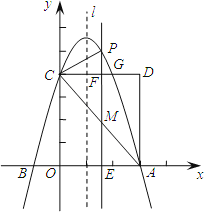
����Ŀ����ͼ��������![]() ��a��0����x����A��B���㣬A������Ϊ��3��0������y�ύ�ڵ�C��0��4������OC��OAΪ��������OADC���������ڵ�G��
��a��0����x����A��B���㣬A������Ϊ��3��0������y�ύ�ڵ�C��0��4������OC��OAΪ��������OADC���������ڵ�G��
��1���������ߵĽ���ʽ��
��2�������ߵĶԳ���l�ڱ�OA��������O��A���㣩��ƽ���ƶ����ֱ�x���ڵ�E����CD�ڵ�F����AC�ڵ�M�����������ڵ�P������M�ĺ�����Ϊm�����ú�m�Ĵ���ʽ��ʾPM�ij���
��3���ڣ�2���������£�����PC������CD�Ϸ��������߲����Ƿ���������ĵ�P��ʹ����P��C��FΪ����������κ���AEM���ƣ������ڣ������ʱm��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��y=-![]() x2+
x2+![]() x+4����2��PM=-
x+4����2��PM=-![]() m2+4m��0��m��3������3�����������ĵ�Pʹ��PFC����AEM���ƣ���ʱm��ֵΪ
m2+4m��0��m��3������3�����������ĵ�Pʹ��PFC����AEM���ƣ���ʱm��ֵΪ![]() ��1��
��1��
��������
�����������1����A��3��0����C��0��4������y=ax2-2ax+c�����ô���ϵ����������������ߵĽ���ʽ��
��2���ȸ���A��C�����꣬�ô���ϵ�������ֱ��AC�Ľ���ʽ���������������ߺ�ֱ��AC�Ľ���ʽ�ֱ��ʾ����P����M�����꣬���ɵõ�PM�ij���
��3��������PFC����AEM����ֱ�ǣ�F��E��Ӧ��������P��C��FΪ����������κ���AEM����ʱ������������������ۣ��١�PFC�ס�AEM���ڡ�CFP�ס�AEM���ɷֱ��ú�m�Ĵ���ʽ��ʾ��AE��EM��CF��PF�ij����������������ζ�Ӧ�ߵı�����г�����ʽ�����m��ֵ��
�����������1����������y=ax2-2ax+c��a��0��������A��3��0������C��0��4����
��![]() ��
��
���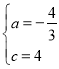 ��
��
�������ߵĽ���ʽΪy=-![]() x2+
x2+![]() x+4��
x+4��
��2����ֱ��AC�Ľ���ʽΪy=kx+b��
��A��3��0������C��0��4����
��![]() ��
��
���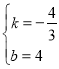 ��
��
��ֱ��AC�Ľ���ʽΪy=-![]() x+4��
x+4��
����M�ĺ�����Ϊm����M��AC�ϣ�
��M���������m��-![]() m+4����
m+4����
����P�ĺ�����Ϊm����P��������y=-![]() x2+
x2+![]() x+4�ϣ�
x+4�ϣ�
����P��������m��-![]() m2+
m2+![]() m+4����
m+4����
��PM=PE-ME=��-![]() m2+
m2+![]() m+4��-��-
m+4��-��-![]() m+4��=-
m+4��=-![]() m2+4m��
m2+4m��
��PM=-![]() m2+4m��0��m��3����
m2+4m��0��m��3����
��3���ڣ�2���������£�����PC����CD�Ϸ��������߲��ִ��������ĵ�P��ʹ����P��C��FΪ����������κ���AEM���ƣ��������£������⣬�ɵ�AE=3-m��EM=-![]() m+4��CF=m������P��C��FΪ����������κ���AEM���ƣ������
m+4��CF=m������P��C��FΪ����������κ���AEM���ƣ������
��P����CD�Ϸ�����PF=-![]() m2+
m2+![]() m+4-4=-
m+4-4=-![]() m2+
m2+![]() m��
m��
����PFC�ס�AEM����PF��AE=FC��EM��
����-![]() m2+
m2+![]() m������3-m��=m����-
m������3-m��=m����-![]() m+4����
m+4����
��m��0��m��3��
��m=![]() ��
��
������CFP�ס�AEM����CF��AE=PF��EM��
��m����3-m��=��-![]() m2+
m2+![]() m������-
m������-![]() m+4����
m+4����
��m��0��m��3��
��m=1��
�������������������ĵ�Pʹ��PFC����AEM���ƣ���ʱm��ֵΪ![]() ��1��
��1��

 ͬ������ϵ�д�
ͬ������ϵ�д�