题目内容
【题目】
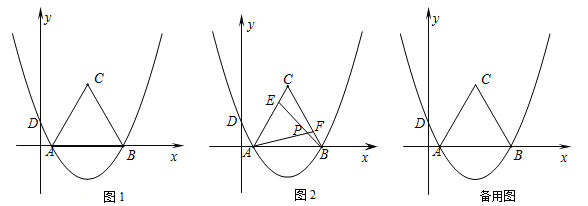
如图1,抛物线经过A(1,0),B(7,0),D(0,![]() ) 三点,以AB为边在x轴上方作等边三角形ABC.
) 三点,以AB为边在x轴上方作等边三角形ABC.
(1)求抛物线的解析式;
(2)在抛物线x轴上方是否存在点M,使S△ABM =![]() S△ABC,若存在,请求出点M坐标;若不存在,请说明理由;
S△ABC,若存在,请求出点M坐标;若不存在,请说明理由;
(3)如图2,E是线段AC上的动点,F是线段BC上的动点,AF与BE相交于点P.
①若CE=BF,试猜想AF与BE的数量关系,请说明理由,并求出∠APB的度数;
②若AF=BE,当点E由A运动到C时,试求点P经过的路径长.
【答案】(1)抛物线的解析式为y=![]() x2-2x+
x2-2x+![]() .(2)M1(9,4),M2(-1,4).(3)①AF=BE,∠APB=120°.
.(2)M1(9,4),M2(-1,4).(3)①AF=BE,∠APB=120°.
【解析】
试题分析:(1)先设出抛物线的解析式,然后将已知点的坐标代入求解即可;
(2)过点C作CK⊥x轴,垂足为K.先求得三角形ABC的面积,从而得到△ABM的面积,依据三角形的面积公式可求得点M的纵坐标为4,由点M在抛物线可知可知y=4,从而可求得对应的x的值,于是得到点M的坐标;
(3)①先证明依据SAS△BEC≌△AFB,由全等三角形的性质可得到AF=BE,接下来证明∠FAB+∠ABP=∠ABC,最后依据三角形的内角和定理可求得∠APB的度数;②如图3所示:设![]() 所在圆的圆心为M,点H在圆M上,连接AM、BM、AH、BH,过点M作MG⊥AB,垂足为G.依据圆的内角四边形的性质和圆周角定理可求得∠AMB的长,接下来,依据等腰三角形三线合一的性质可得到AG=3,∠AMG=60°,然后依据特殊锐角三角函数值可求得AM的长,最后依据扇形的弧长公式求解即可;如图4所示:当AE=BF时.依据SAS可证明△AEB≌△BAF,从而得到∠PAB=∠PBA,故此可知点P在AB的垂直平分线上,最后依据特殊锐角三角函数求得CN的长即可.
所在圆的圆心为M,点H在圆M上,连接AM、BM、AH、BH,过点M作MG⊥AB,垂足为G.依据圆的内角四边形的性质和圆周角定理可求得∠AMB的长,接下来,依据等腰三角形三线合一的性质可得到AG=3,∠AMG=60°,然后依据特殊锐角三角函数值可求得AM的长,最后依据扇形的弧长公式求解即可;如图4所示:当AE=BF时.依据SAS可证明△AEB≌△BAF,从而得到∠PAB=∠PBA,故此可知点P在AB的垂直平分线上,最后依据特殊锐角三角函数求得CN的长即可.
试题解析:(1)设抛物线的解析式为y=ax2+bx+![]() .
.
∵将点A、B的坐标代入得: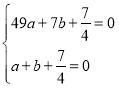 ,解得:a=
,解得:a=![]() ,b=-2,
,b=-2,
∴抛物线的解析式为y=![]() x2-2x+
x2-2x+![]() .
.
(2)存在点M使得S△AMB=![]() S△ABC.
S△ABC.
如图1所示:过点C作CK⊥x轴,垂足为K.
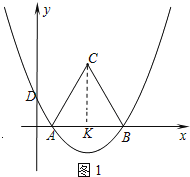
∵△ABC为等边三角形,
∴AB=BC=AC=6,∠ACB=60°.
∵CK⊥AB,
∴KA=BK=3,∠ACK=60°.
∴CK=3![]() .
.
∴S△ABC=![]() ABCK=
ABCK=![]() ×6×3
×6×3![]() =9
=9![]() .
.
∴S△ABM=![]() ×9
×9![]() =12.
=12.
设M(x,![]() x2-2x+
x2-2x+![]() ).
).
∴![]() AB|yM|=12,即
AB|yM|=12,即![]() ×6×(
×6×(![]() x2-2x+
x2-2x+![]() )=12.
)=12.
解得x1=9,x2=-1.
∴M1(9,4),M2(-1,4).
(3)①AF=BE,∠APB=120°.
理由:如图2所示;
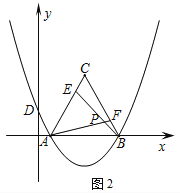
∵△ABC为等边三角形,
∴BC=AB,∠C=∠ABF.
∵在△BEC和△AFB中
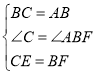 ,
,
∴△BEC≌△AFB.
∴AF=BE,∠CBE=∠BAF.
∴∠FAB+∠ABP=∠ABP+∠CBE=∠ABC=60°.
∴∠APB=180°-∠PAB-∠ABP=180°-60°=120°.
②如图3所示:当CE=FB时.
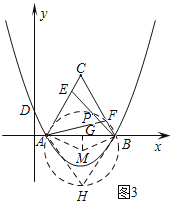
∵由①可知:∠APB=120°,
∴点P的运动轨迹是一条弧.
设![]() 所在圆的圆心为M,点H在圆M上,连接AM、BM、AH、BH,过点M作MG⊥AB,垂足为G.
所在圆的圆心为M,点H在圆M上,连接AM、BM、AH、BH,过点M作MG⊥AB,垂足为G.
∵∠APB=120°,
∴∠AHB=60°.
∴∠AMB=120°.
∵AM=MB,MG⊥AB,
∴AG=BG=3,∠AMG=∠BMG=60°.
∴![]() ,即
,即![]() .
.
∴AM=2![]() .
.
∴点P运动的路径=![]() .
.
如图4所示:当AE=BF时.
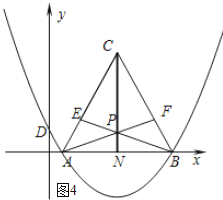
∵在△ABE和△BAF中
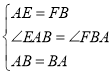 ,
,
∴△ABE≌△BAF.
∴AF=EB,∠FAB=∠EBA.
∴AP=BP.
∴点P在AB的垂直平分线上.
∴点P运动的路线=NC=3![]() .
.
∴点P经过的路径长为![]() 或3
或3![]() .
.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案