题目内容
【题目】如图所示,△ABC的外接圆圆心O在AB上,点D是BC延长线上一点,DM⊥AB于M,交AC于N,且AC=CD.CP是△CDN的ND边的中线.
(1)求证:△ABC≌△DNC;
(2)试判断CP与⊙O的位置关系,并证明你的结论。
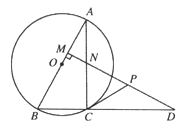
【答案】(1)证明见解析;(2)CP是⊙O的切线.证明见解析
【解析】
试题分析:(1)由题意要证全等,根据圆周角定理及等量代换得到全等条件即可解答;
(2)连接OC,利用等量代换证明角OCP为直角即可解答.
试题解析:(1)∵DM⊥AB,
∴∠AMN=90°,
∴∠MAN=90°-∠MNA,
又∵∠MNA=∠CND,
又∵∠D=90°-∠CND,
∴∠MAN=∠D,
又∵AC=CD,
AB为⊙O的直径,
∴∠ACB=90°=∠NCD,
∴△ABC≌△DNC(ASA)
(2)CP是⊙O的切线.证明如下:
连接OC
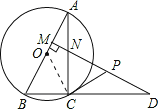
∵CP为△CND的中线,
∴CP=PD=NP,
∴∠PCD=∠D=∠MAN.
又∠PCD+∠NCP=90°,∠MAN+∠MBC=90°,
∴∠NCP=∠MBC,
又∵OA=OC,
∴∠OCA=∠MAN
∴∠OCA+∠NCP=∠MAN+∠MBC=90°
∴CP是⊙O的切线.

练习册系列答案
相关题目