题目内容
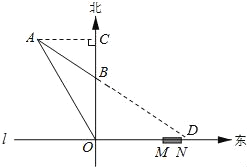
【题目】如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距20![]() 千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据:![]() ,
,![]() )
)

【答案】(1)30千米/时;(2) 该轮船不改变航向继续航行,不能行至码头MN靠岸.
【解析】
试题分析:(1))过点A作AC⊥OB于点C.可知△ABC为直角三角形.根据勾股定理解答.
(2)延长AB交l于D,比较OD与AM、AN的大小即可得出结论.
试题解析:(1)过点A作AC⊥OB于点C.由题意,得
OA=![]() 千米,OB=20千米,∠AOC=30°.
千米,OB=20千米,∠AOC=30°.
∴![]() (千米).
(千米).
∵在Rt△AOC中,OC=OAcos∠AOC=![]() =30(千米).
=30(千米).
∴BC=OC-OB=30-20=10(千米).
∴在Rt△ABC中,![]() =20(千米).
=20(千米).
∴轮船航行的速度为:![]() (千米/时).
(千米/时).
(2)如果该轮船不改变航向继续航行,不能行至码头MN靠岸.
理由:延长AB交l于点D.
∵AB=OB=20(千米),∠AOC=30°.
∴∠OAB=∠AOC=30°,∴∠OBD=∠OAB+∠AOC=60°.
∴在Rt△BOD中,OD=OBtan∠OBD=20×tan60°=![]() (千米).
(千米).
∵![]() >30+1,
>30+1,
∴该轮船不改变航向继续航行,不能行至码头MN靠岸.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目