Question

【题目】如图，半径为5的⊙P与y轴交于点M（0，﹣4），N（0，﹣10），点P的坐标为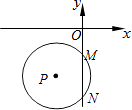

Answer 1

【答案】（﹣4，﹣7）
【解析】解：过P作PQ⊥y轴，与y轴交于Q点，连接PM，∴Q为MN的中点，
∵M（0，﹣4），N（0，﹣10），
∴OM=4，ON=10，
∴MN=10﹣4=6，
∴MQ=NQ=3，OQ=OM+MQ=4+3=7，
在Rt△PMQ中，PM=5，MQ=3，
根据勾股定理得：PQ= = =4，
∴P（﹣4，﹣7）．
所以答案是：（﹣4，﹣7）．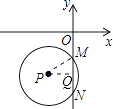

【考点精析】利用勾股定理的概念和垂径定理对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．