题目内容
【题目】如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E,F,连接EF. 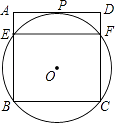
(1)求证:PF平分∠BFD;
(2)若tan∠FBC= ![]() ,DF=
,DF= ![]() ,求EF的长.
,求EF的长.
【答案】
(1)证明:连接OP、BF、PF.
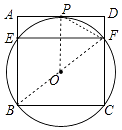
∵⊙O与AD相切于点P,
∴PO⊥AD,
∵四边形ABCD是正方形,
∴CD⊥AD,
∴OP∥CD,
∴∠PFD=∠OPF,
∵OP=OF,
∴∠OPF=∠OFP,
∴∠OFP=∠PFD,
∴PF平分∠BFD
(2)解:∵∠C=90°,
∴BF是⊙O的直径,
∴∠BEF=90°,
∴四边形BCFE是矩形,
∴EF=BC,
∵tan∠FBC= ![]() ,设FC=3x,则BC=4x,
,设FC=3x,则BC=4x,
∵BC=DC,
∴4x=3x+ ![]() ,
,
∴x= ![]() ,
,
∴EF=BC=4 ![]() .
.
【解析】(1)连接OP、BF、PF.由OP∥CD,推出∠PFD=∠OPF,由OP=OF,推出∠OPF=∠OFP,即可推出∠OFP=∠PFD.(2)首先证明四边形BCFE是矩形,推出EF=BC,由tan∠FBC= ![]() ,设FC=3x,则BC=4x,由BC=DC,可得方程4x=3x+
,设FC=3x,则BC=4x,由BC=DC,可得方程4x=3x+ ![]() ,解方程即可解决问题.
,解方程即可解决问题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目