题目内容
【题目】如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A在x轴上,AB=AC,∠BAC=90°,且A(2,0)、B(3,3),BC交y轴于M,
(1)求点C的坐标;
(2)连接AM,求△AMB的面积;
(3)在x轴上有一动点P,当PB+PM的值最小时,求此时P的坐标.

【答案】(1)C的坐标是(﹣1,1);(2)![]() ;(3)点P的坐标为(1,0).
;(3)点P的坐标为(1,0).
【解析】
(1)作CD⊥x轴于D,BE⊥x轴于E,证明![]() ≌
≌![]() ,根据全等三角形的性质得到CD=AE,AD=BE,求出点C的坐标;
,根据全等三角形的性质得到CD=AE,AD=BE,求出点C的坐标;
(2)利用待定系数法求出直线BC的解析式,得到OM的长,根据梯形的面积公式、三角形的面积公式计算,得到答案;
(3)根据轴对称的最短路径问题作出点P,求出直线B![]() 的解析式,根据x轴上点的坐标特征求出点P的坐标.
的解析式,根据x轴上点的坐标特征求出点P的坐标.
解:(1)如图,作CD⊥x轴于D,BE⊥x轴于E,

∴∠CAD+∠DCA=90°,
∵∠BAC=90°,
∴∠CAD+∠BAE=90°,
∴∠BAE=∠ACD,
在![]() 和
和![]() 中,
中,
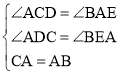 ,
,
∴![]() ≌
≌![]() (AAS),
(AAS),
∴CD=AE,AD=BE,
∵A(2,0)、B(3,3),
∴OA=2,OE=BE=3,
∴CD=AE=1,OD=AD﹣OA=1,
∴C的坐标是(﹣1,1);
(2)如图,作BE⊥x轴于E,
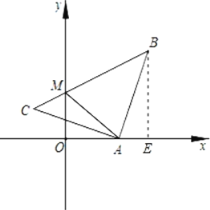
设直线BC的解析式为y=kx+b,
∵B点的坐标为(3,3),C点的坐标是(﹣1,1),
∴![]() ,
,
解得,![]() ,
,
∴直线BC的解析式为y=![]() x+
x+![]() ,
,
当x=0时,y=![]() ,
,
∴OM=![]() ,
,
∴![]() 的面积=梯形MOEB的面积﹣
的面积=梯形MOEB的面积﹣![]() 的面积﹣
的面积﹣![]() 的面积
的面积
=![]() ×(
×(![]() +3)×3﹣
+3)×3﹣![]() ×2×
×2×![]() ﹣
﹣![]() ×1×3
×1×3
=![]() ;
;
(3)如图,作M关于x轴的对称点![]() (0,﹣
(0,﹣![]() ),连接B
),连接B![]() ,交x轴于点P,此时PB+PM=PB+P
,交x轴于点P,此时PB+PM=PB+P![]() =B
=B![]() 的值最小,
的值最小,
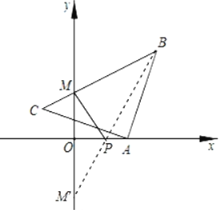
设直线B![]() 的解析式为y=mx+n,
的解析式为y=mx+n,
则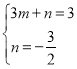 ,
,
解得,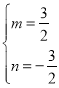 ,
,
∴直线B![]() 的解析式为y=
的解析式为y=![]() x﹣
x﹣![]() ,
,
点P在x轴上,当y=0时,x=1,
∴点P的坐标为(1,0).

 阅读快车系列答案
阅读快车系列答案



