��Ŀ����
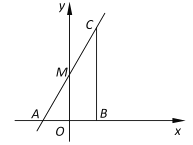
����Ŀ����һ�����ǰ��е�����ֱ�����ǰ��ֱ�Ƕ���C����ͼ��ʽ������һ��������ʾ����A��60�㣬��D��30�㣬��E����B��45�㣮
(1)������DCB��45�㣬���ACB�Ķ���Ϊ�� ����
������ACB��140�㣬���DCE�Ķ���Ϊ�� ����
(2)��(1)�����ACB���DCE��������ϵ����˵�����ɣ�
(3)����ACE��90���ҵ�E��ֱ��AC���Ϸ�ʱ�������������dz���һ�����ƽ��ʱ����ֱ��д����ACE�Ƕ����п��ܵ�ֵ(����˵������)��

���𰸡�(1)��135�㣻��40�㣻(2)��ACB+��DCE��180�㣬���ɼ�������(3)30�㡢45�㣮
��������
(1)�ٸ���ֱ�����ǰ�����ʽ����DCB��45�����ɵó���ACB�Ķ�����
���ɡ�ACB=140�㣬��ECB=90�㣬�ɵó���ACE�Ķ����������ó���DCE�Ķ�����
(2)���ݢ��еĽ��ۿ�������룬���ɡ�ACB=��ACD+��DCB����ACB+��DCE=90��+��DCB+��DCE�ɵó����ۣ�
(3)��CB��AD��EB��AC��������������ۼ���.
(1)�١ߡ�DCB��45������ACD��90����
���ACB����DCB+��ACD��45��+90����135����
�ʴ�Ϊ��135����
�ڡߡ�ACB��140������ECB��90����
���ACE��140����90����50����
���DCE��90������ACE��90����50����40����
�ʴ�Ϊ��40����
(2)���룺��ACB+��DCE��180����
�������£��ߡ�ACE��90������DCE��
���ߡ�ACB����ACE+90����
���ACB��90������DCE+90����180������DCE��
����ACB+��DCE��180����
(3)30����45����
���ɣ���CB��ADʱ����ͼ1����
����AFC=��FCB=90����
����A=60����
����ACE��90��-��A=30����
��EB��ACʱ����ͼ2����
���ACE����E=45����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�