题目内容
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D. 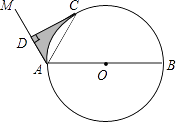
(1)求证:CD是⊙O的切线;
(2)若∠ACD=30°,AD=4,求图中阴影部分的面积.
【答案】
(1)证明:连接OC.
∵OA=OC.
∴∠OAC=∠OCA,
∵∠MAC=∠OAC,
∴∠MAC=∠OCA,
∴OC∥AM,
∵CD⊥AM,
∴OC⊥CD,
∴CD是⊙O的切线

(2)解:在RT△ACD中,∵∠ACD=30°,AD=4,∠ADC=90°,
∴AC=2AD=8,CD= ![]() AD=4
AD=4 ![]() ,
,
∵∠MAC=∠OAC=60°,OA=OC,
∴△AOC是等边三角形,
∴S阴=S△ACD﹣(S扇形OAC﹣S△AOC)
= ![]() ×4×4
×4×4 ![]() ﹣(
﹣( ![]() ﹣
﹣ ![]() ×82)
×82)
=24 ![]() ﹣
﹣ ![]() π
π
【解析】(1)先证明OC∥AM,由CD⊥AM,推出OC⊥CD即可解决问题.(2)根据S阴=S△ACD﹣(S扇形OAC﹣S△AOC)计算即可.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目