Question

【题目】A、B两组卡片共5张，A中三张分别写有数字2，4，6，B中两张分别写有3，5．它们除了数字外没有任何区别．
（1）随机地从A中抽取一张，求抽到数字为2的概率；
（2）随机地分别从A、B中各抽取一张，请你用画树状图或列表的方法表示所有等可能的结果，现制定这样一个游戏规则：若选出的两数之积为3的倍数，则甲获胜；否则乙获胜．请问这样的游戏规则对甲乙双方公平吗？为什么？
（3）如果不公平请你修改游戏规则使游戏规则对甲乙双方公平．

Answer 1

【答案】
（1）解：P（抽到数字为2）=1/3
（2）解：不公平，理由如下．画树状图如下：

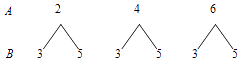
（3）解：从树状图中可知共有6个等可能的结果，而所选出的两数之积为3的倍数的机会有4个．

∴P（甲获胜） ，而P（乙获胜） ，

∵P（甲获胜）＞P（乙获胜）

∴这样的游戏规则对甲乙双方不公平

【解析】（1）根据概率的定义列式即可；（2）画出树状图，然后根据概率的意义分别求出甲、乙获胜的概率，从而得解；（3）根据游戏的公平性进行解答即可．
【考点精析】根据题目的已知条件，利用列表法与树状图法和概率公式的相关知识可以得到问题的答案，需要掌握当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率；一般地，如果在一次试验中，有n种可能的结果，并且它们发生的可能性都相等，事件A包含其中的m中结果，那么事件A发生的概率为P（A）=m/n．