题目内容
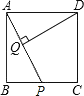
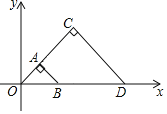
【题目】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:3,∠OCD=90°,CO=CD.若B(2,0),则点C的坐标为( )
A.(3,3)B.(2,4)C.(![]() ,2
,2![]() )D.(4,4)
)D.(4,4)
【答案】A
【解析】
首先利用等腰直角三角形的性质得出A点坐标,再利用位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(﹣kx,ky),进而求出即可.
∵∠OAB=∠OCD=90°,CO=CD,Rt△OAB与Rt△OCD是位似图形,点B的坐标为(2,0),
∴BO=2,则AO=AB=![]() ,
,
∴A(1,1),
∵等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:3,
∴点C的坐标为:(3,3).
故选:A.

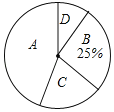
【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调査(问卷调査表如图所示),将调査结果整理后绘制例图1、图2两幅均不完整的统计图表.
最受欢迎的校本课程调查问卷
您好!这是一份关于您最喜欢的校本课程问卷调查表,请在表格中选择一个(只能选一个)您最喜欢的课程选项,在其后空格内打“√”,非常感谢您的合作.
选项 | 校本课程 | |
A | 3D打印 | |
B | 数学史 | |
C | 诗歌欣赏 | |
D | 陶艺制作 |
校本课程 | 频数 | 频率 |
A | 36 | 0.45 |
B | 0.25 | |
C | 16 | b |
D | 8 | |
合计 | a | 1 |
请您根据图表中提供的信息回答下列问题:
(1)统计表中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调査结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.