题目内容
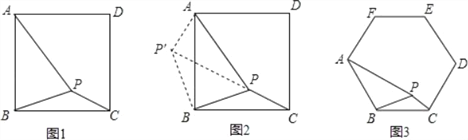
【题目】如图1，在正方形ABCD内有一点P，PA=3，PB=2，PC=1，求∠BPC的度数．
分析：根据已知条件比较分散的特点，我们可以通过旋转变换将分散的已知条件集中在一起，于是将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连结PP′，这时再分别求出∠BP′P和∠AP′P的度数．
解答：（1）请你根据以上分析再通过计算求出图2中∠BPC的度数；
（2）如图3，若在正六边形ABCDEF内有一点P，且PA=2
，PB=4，PC=2，求∠BPC的度数．
【答案】（1）135°；（2）120°.
【解析】试题分析：(1)根据旋转的性质得到∠P′BP=90°，BP′=BP=2 ，P′A=PC=1，∠BP′A=∠BPC，则△BPP′为等腰直角三角形，根据等腰直角三角形的性质得PP′= 
，PB=2，∠BP′P=45°，利用勾股定理的逆定理可得到△APP′为直角三角形，且∠AP′P=90°，则∠BPC=∠BP′A=45°+90°=135°；（2）把△BPC绕点B逆时针旋转120°，得到了△BP′A，根据旋转的性质得到∠P′BP=120°，BP′=BP=4，P′A=PC=2，∠BP′A=∠BPC，则∠BP′P=∠BPP′=30°，得到P′H=PH，利用含30°的直角三角形三边的关系得到BH=
BP′=2，P′H=
BH=2
，得到P′P=2P′H=4
，再利用勾股定理的逆定理可得到△APP′为直角三角形，且∠AP′P=90°，于是有∠BPC=∠BP′A=30°+90°=120°.
试题解析：
（1）如图2．
∵△BPC绕点B逆时针旋转90°，得到了△BP′A，
∴∠P′BP=90°，BP′=BP=2 ，P′A=PC=1，∠BP′A=∠BPC，
∴△BPP′为等腰直角三角形，
∴PP′=
PB=2，∠BP′P=45°，
在△APP′中，AP=3
，PP′=2，AP′=1，
∵32=（2
）2+12，
∴AP2=PP′2+AP′2，
∴△APP′为直角三角形，且∠AP′P=90°
∴∠BP′A=45°+90°=135°，
∴∠BPC=∠BP′A=135°；
（2）如图3．
∵六边形ABCDEF为正六边形，
∴∠ABC=120°，
把△BPC绕点B逆时针旋转120°，得到了△BP′A，
∴∠P′BP=120°，BP′=BP=4，P′A=PC=2，∠BP′A=∠BPC，
∴∠BP′P=∠BPP′=30°，
过B作BH⊥PP′于H，
∵BP′=BP，
∴P′H=PH，
在Rt△BP′H中，∠BP′H=30°，BP′=4，
∴BH=
BP′=2，P′H=
BH=2
，
∴P′P=2P′H=4
，
在△APP′中，AP=2
，PP′=4
，AP′=2，
∵（2
）2=（4
）2+22，
∴AP2=PP′2+AP′2，
∴△APP′为直角三角形，且∠AP′P=90°，
∴∠BP′A=30°+90°=120°，
∴∠BPC=120°．
