Question

【题目】如图，A，O，B三点在同一直线上，∠BOD与∠BOC互补．

（1）试判断∠AOC与∠BOD之间有怎样的数量关系，写出你的结论，并加以证明；

（2）OM平分∠AOC，ON平分∠AOD，①依题意，将备用图补全；

② 若∠MON=40°，求∠BOD的度数．

Answer 1

【答案】（1）∠AOC =∠BOD ；（2）①答案见解析；②∠BOD =50°．

【解析】试题分析：（1）根据同角的补角相等即可得出结论；

（2）①根据题意画出图形；

②由角平分线的定义和平角的定义解答即可．

试题解析：解：（1）∠AOC =∠BOD ．理由如下：

∵ 点A，O，B三点在同一直线上， ∴ ∠AOC +∠BOC = 180°．

∵∠BOD与∠BOC互补，∴ ∠BOD +∠BOC = 180°，∴ ∠AOC =∠BOD．

（2）①补全图形，如图所示．

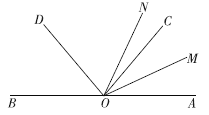
②设∠AOM =α．

∵ OM平分∠AOC，∴ ∠AOC =2∠AOM =2α．

∵ ∠MON=40°，∴ ∠AON =∠MON +∠AOM =40°+ α．

∵ ON平分∠AOD，∴ ∠AOD =2∠AON =80° +2α．

由（1）可得 ∠BOD=∠AOC=2α，∵∠BOD +∠AOD =180°，∴ 2α+ 80 +2α=180°，∴ 2α=50°，∴ ∠BOD =50°．