题目内容
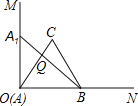
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的发散点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=3r,则称P′为点P关于⊙C的发散点.下图为点P及其关于⊙C的发散点P′的示意图.特别地,当点P′与圆心C重合时,规定CP′=0.
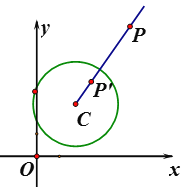
根据上述材料,请你解决以下问题:
(1)当⊙O的半径为1时,
①在点![]() 关于⊙O的发散点的是点 ;其对应发散点的坐标是 ;
关于⊙O的发散点的是点 ;其对应发散点的坐标是 ;
②点P在直线![]() 上,若点P关于⊙O的发散点P′存在,且点P′不在x轴上,求点P的横坐标m的取值范围;
上,若点P关于⊙O的发散点P′存在,且点P′不在x轴上,求点P的横坐标m的取值范围;
(2)⊙C的圆心C在x轴上,半径为1,直线![]() 与x轴、y轴分別交于点A,B.若线段AB上存在点P,使得点P关于⊙C的发散点P′在⊙C的内部,请直接写出圆心C的横坐标n的取值范围 .
与x轴、y轴分別交于点A,B.若线段AB上存在点P,使得点P关于⊙C的发散点P′在⊙C的内部,请直接写出圆心C的横坐标n的取值范围 .
【答案】(1)N,T ![]() ,(0,0);(2)
,(0,0);(2)![]() <m<3.
<m<3.
【解析】
(1)①根据发散点的定义依次进行判断即可;②由OP≤3r=3,得出OP2≤9,设P(m,![]() ),由勾股定理得出OP2=m2+(
),由勾股定理得出OP2=m2+(![]() )2=4m2-18m+27≤9,解不等式得出
)2=4m2-18m+27≤9,解不等式得出![]() ≤m≤3.再分别将m=
≤m≤3.再分别将m=![]() 与3代入检验即可;
与3代入检验即可;
(2)先由已知条件求出A(9,0),B(0,3![]() ),则
),则![]() ,∠OBA=60°,∠OAB=30°.再设C(n,0),分两种情况进行讨论:①C在OA上;②C在A点右侧.
,∠OBA=60°,∠OAB=30°.再设C(n,0),分两种情况进行讨论:①C在OA上;②C在A点右侧.
解:(1)①设点M(3,1)的发散点为M’,则根据发散点的定义可得:OM+OM’=3,
![]() OM=
OM=![]() =
=![]() ,
,
∴OM’=3-![]() <0.
<0.
故不符合题意,点M(3,1)不存在关于⊙O的发散点.
同理可求得:设点N![]() 关于⊙O的发散点为N’,则
关于⊙O的发散点为N’,则
ON+ON’=3,
∴ON’=3-![]() =
=![]()
∴点N![]() 关于⊙O的发散点N’的坐标为
关于⊙O的发散点N’的坐标为![]() ;
;
设点T(2![]() ,1) 关于⊙O的发散点为T’,
,1) 关于⊙O的发散点为T’,
则OT+OT’=3,
∴OT’=3-![]() =0
=0
∴点T(2![]() ,1) 关于⊙O的发散点为T’的坐标为(0,0)
,1) 关于⊙O的发散点为T’的坐标为(0,0)
故答案为:N,T ![]() ,(0,0);
,(0,0);
![]() 设点P的坐标为(m,
设点P的坐标为(m,![]() ),
),
∵OP≤3,
∴![]() ≤9.
≤9.
∴![]() +
+![]() ≤9
≤9
整理得:![]() -
-![]() ≤0
≤0
解得:![]() ≤m≤3.
≤m≤3.
又∵点P不在轴上,
∴点P的横坐标m的取值范围![]() <m<3;
<m<3;
(2)令y=0,则![]() ,解得x=9,
,解得x=9,
∴A的坐标为(9,0)
令x=0,则y=3![]() ,
,
∴点B的坐标为(0,3![]() ).
).
∴![]() ,
,
∴∠OBA=60°,∠OAB=30°.
设C的坐标为(n,0)
当点C在OA上时,作CD⊥AB于D,则
CD≤CP≤3r=3
∴AC=2CD≤6
∴9-n≤6解得n≥3
当点C在点A右边时,AC的最大值为3.
∴C的横坐标n≤12.
综上所述,圆心C的横坐标的取值范围是![]() ≤m≤3.
≤m≤3.