题目内容
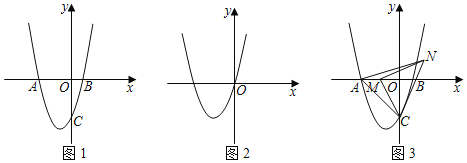
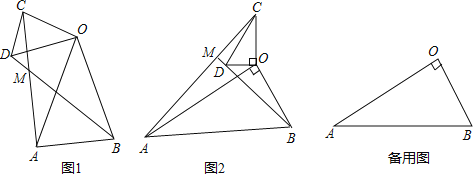
【题目】如图1,在Rt△ABC中,∠ABC=90°,AB=BC=4,点D、E分别是边AB、AC的中点,连接DE,将△ADE绕点A按顺时针方向旋转,记旋转角为α,BD、CE所在直线相交所成的锐角为β.
(1)问题发现当α=0°时,![]() =_____;β=_____°.
=_____;β=_____°.
(2)拓展探究
试判断:当0°≤α<360°时,![]() 和β的大小有无变化?请仅就图2的情形给出证明.
和β的大小有无变化?请仅就图2的情形给出证明.
(3)在△ADE旋转过程中,当DE∥AC时,直接写出此时△CBE的面积.
【答案】(1)![]() ,45;(2)
,45;(2)![]() 和β的大小无变化;(3)△BCE的面积为4或12.
和β的大小无变化;(3)△BCE的面积为4或12.
【解析】
(1)利用等腰直角三角形的性质,线段的中点的定义即可判断.
(2)结论:![]() 和β的大小无变化.如图2中,延长CE交AB于点O,交BD于K.证明△DAB∽△EAC,即可解决问题.
和β的大小无变化.如图2中,延长CE交AB于点O,交BD于K.证明△DAB∽△EAC,即可解决问题.
(3)分两种情形:①当点D在线段AB上时,②当点D在线段BA的延长线上时,分别求解即可.
解:(1)如图1中,
∵∠B=90°,BA=BC,
∴∠A=45°,AC=![]() AB,
AB,
∵点D、E分别是边AB、AC的中点,
∴BD=![]() AB,EC=
AB,EC=![]() AC,
AC,
∴![]() =
=![]() ,β=45°,
,β=45°,
故答案为![]() ,45.
,45.
(2)结论:![]() 和β的大小无变化.
和β的大小无变化.
理由:如图2中,延长CE交AB于点O,交BD于K.

∵AE=![]() AD,AC=
AD,AC=![]() AB,
AB,
∴![]() =
=![]() ,
,
∴![]() ,
,
∵∠DAE=∠BAC,
∴∠DAB=∠EAC,
∴△DAB∽△EAC,
∴![]() =
=![]() =
=![]() ,∠OBK=∠OCA,
,∠OBK=∠OCA,
∵∠BOK=∠COA,
∠BKO=∠CAO=45°,
∴![]() 和β的大小无变化.
和β的大小无变化.
(3)当点D在线段AB上时,S△BCE=![]() ×4×2=4,
×4×2=4,
当点D在线段BA的延长线上时,S△BCE=![]() ×4×6=12.
×4×6=12.
综上所述,△BCE的面积为4或12.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目