题目内容
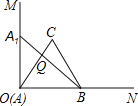
【题目】已知∠MON=90°,等边三角形ABC的一个顶点B是射线ON上的一定点,顶点A于点O重合,顶点C在∠MON内部
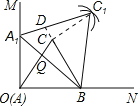
(1)当点A在射线OM上移动到A1时,连接A1B,请在∠MON内部作出以A1B为一边的等边三角形A1BC1(保留作图痕迹,不写作法);
(2)设A1B与OC交于点Q,BC的延长线与A1C1交于点D.求证:△BCQ∽△BA1D;
(3)连接CC1,试猜想∠BCC1为多少度,并证明你的猜想.
【答案】(1)详见解析;(2)详见解析;(3)∠BCC1=90°,理由详见解析.
【解析】
(1)分别以B、A1为圆心,A1B长为半径画弧,两弧交于一点C1,连接A1C1,BC1即可;
(2)根据条件可以得到∠BCQ=∠BA1D=60°,∠A1BD=∠QBC,即可证出△BCQ∽△BA1D;
(3)首先证明∠ABA1=∠CBC1,再利用SAS定理证出△A1BA≌△C1BC,即可得到∠BCC1=∠BAA1=90°.
(1)如图所示:
(2)∵△ACB和△A1C1B都是等边三角形,
∴∠BCQ=∠BA1D=60°,
∵∠A1BD=∠QBC,
∴△BCQ∽△BA1D;
(3)猜想∠BCC1=90°,
∵△ACB和△A1C1B都是等边三角形,
∴∠CBA=∠A1BC1=60°,A1B=C1B,AB=CB,
∴∠ABA1=∠CBC1,
在△A1BA和△C1BC中: 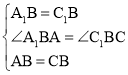 ,
,
∴△A1BA≌△C1BC(SAS),
∴∠BCC1=∠BAA1=90°.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
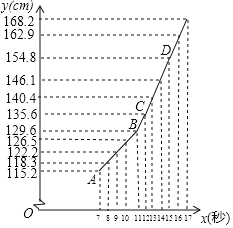
口算题卡河北少年儿童出版社系列答案【题目】数学兴趣小组为了研究中小学男生身高y(cm)和年龄x(岁)的关系,从某市官网上得到了该市2017年统计的中小学男生各年龄组的平均身高,见下表:如图已经在直角坐标系中描出了表中数据对应的点,并发现前5个点大致位于直线AB上,后7个点大致位于直线CD上.
年龄组x | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
男生平均身高y | 115.2 | 118.3 | 122.2 | 126.5 | 129.6 | 135.6 | 140.4 | 146.1 | 154.8 | 162.9 | 168.2 |
(1)该市男学生的平均身高从 岁开始增加特别迅速.
(2)求直线AB所对应的函数表达式.
(3)直接写出直线CD所对应的函数表达式,假设17岁后该市男生身高增长速度大致符合直线CD所对应的函数关系,请你预测该市18岁男生年龄组的平均身高大约是多少?