题目内容
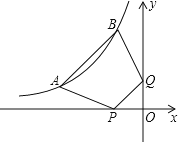
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,且
边上一点,且![]() .点
.点![]() 是直线
是直线![]() 上一点且在点
上一点且在点![]() 的右侧,
的右侧,![]() ,点
,点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向以每秒1个单位长度的速度运动,设运动时间为
方向以每秒1个单位长度的速度运动,设运动时间为![]() 秒.以
秒.以![]() 为圆心,
为圆心,![]() 为半径作半圆
为半径作半圆![]() ,交直线
,交直线![]() 分别于点
分别于点![]() ,
,![]() (点
(点![]() 在
在![]() 的左侧).
的左侧).
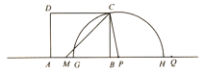
(1)当![]() 秒时,
秒时,![]()
![]() 的长等于__________,
的长等于__________,![]() __________秒时,半圆
__________秒时,半圆![]() 与
与![]() 相切;
相切;
(2)当点![]() 与点
与点![]() 重合时,求半圆
重合时,求半圆![]() 被矩形
被矩形![]() 的对角线
的对角线![]() 所截得的弦长;
所截得的弦长;
(3)若![]() ,求扇形
,求扇形![]() 的面积.
的面积.
(参考数据:![]() ,
,![]() ,
,![]() )
)
【答案】(1)![]() ,
,![]() ;(2)当点
;(2)当点![]() 与点
与点![]() 重合时,半圆
重合时,半圆![]() 被矩形
被矩形![]() 的对角线
的对角线![]() 所截得的弦长为
所截得的弦长为![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)先根据线段的和差求出BP的长,再根据勾股定理即可求出PC的长;先根据圆的性质、勾股定理求出BP的长,再根据线段的和差求出PQ的长,由此即可求出t的值;
(2)如图3(见解析),先在![]() 中,求出
中,求出![]() ,从而可得
,从而可得![]() ,再根据直角三角形的性质求出
,再根据直角三角形的性质求出![]() ,然后根据正弦三角函数值求出CF的长,最后根据垂径定理即可得;
,然后根据正弦三角函数值求出CF的长,最后根据垂径定理即可得;
(3)先依题意分两种情况,再分别根据三角形的外角性质求出![]() 的度数,然后根据直角三角形的性质求出PC的长,最后根据扇形的面积公式求解即可得.
的度数,然后根据直角三角形的性质求出PC的长,最后根据扇形的面积公式求解即可得.
(1)![]() 四边形ABCD是矩形
四边形ABCD是矩形
![]()
![]()
当![]() 秒时,
秒时,![]()
![]()
![]()
若半圆![]() 与
与![]() 相切,则点P在线段AB上,且
相切,则点P在线段AB上,且![]()
设![]() ,则
,则![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
![]()
![]()
![]()
故答案为:![]() ,
,![]() ;
;
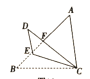
(2)如图3,过点![]() 作
作![]() 于
于![]()
在![]() 中,
中,![]()
![]() ,
,![]()
![]() 在
在![]() 中,
中,![]()
![]() ,即
,即![]()
![]()
由垂径定理可得:![]()
故当点![]() 与点
与点![]() 重合时,半圆
重合时,半圆![]() 被矩形
被矩形![]() 的对角线
的对角线![]() 所截得的弦长为
所截得的弦长为![]() ;
;
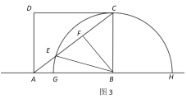
(3)若![]() ,分以下两种情况:
,分以下两种情况:
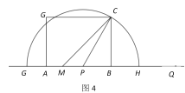
①如图4,![]()
![]()
在![]() 中,
中,![]()
则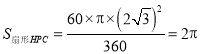
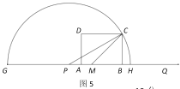
②如图5,![]()
![]()
在![]() 中,
中,![]()
则![]()
综上,扇形![]() 的面积为
的面积为![]() 或
或![]() .
.

练习册系列答案
相关题目