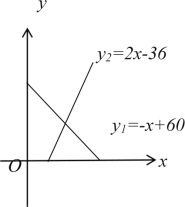题目内容
【题目】(1)因式分解:![]() ___________.
___________.
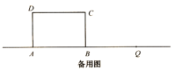
(2)如图,在平面直角坐标系中,A(6,0),B(0,2![]() ),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为_______.扇形BAC的面积为______.
),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为_______.扇形BAC的面积为______.
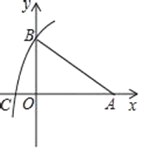
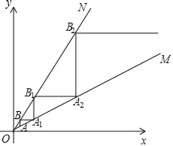
(3)在平面直角坐标系中,点![]() 在射线OM上,点
在射线OM上,点![]() 在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,则点B1的纵坐标为________,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_______.
在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,则点B1的纵坐标为________,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_______.
【答案】b(a+1)(a-1) (6-4![]() ,0) 4π 4 22021
,0) 4π 4 22021
【解析】
(1)先提取公因式b,再对余下的多项式利用平方差公式继续分解.
(2)根据勾股定理求出AB,根据坐标与图形性质求得OC的长即可求得点C的坐标,然后求得∠BAO的度数,利用扇形面积公式计算即可.
(3)根据题意,分别找到AB、A1B1、A2B2……及 BA1、B1A2、B2A3……线段长度递增规律即可
(1)a2b-b=b(a2-1)=b(a+1)(a-1).
故答案为:b(a+1)(a-1).
(2)由题意得,OB=2![]() ,OA=6,
,OA=6,
∴AB=![]() ,
,
则AC=4![]() ,
,
∴OC=AC-OA=4![]() -6,
-6,
∴点C坐标为(6-4![]() ,0),
,0),
∵tanA=![]() ,
,
∴∠A=30°,
∴S扇形ABC=![]() =4π,
=4π,
故答案为:(6-4![]() ,0),4π.
,0),4π.
(3)由已知可知
点A、A1、A2、A3……A2020各点在正比例函数y=![]() x的图象上
x的图象上
点B、B1、B2、B3……B2020各点在正比例函数y=![]() x的图象上
x的图象上
两个函数相减得到横坐标不变的情况下两个函数图象上点的纵坐标的差为![]() x ①;
x ①;
当A(B)点横坐标为![]() 时,由①AB=1,则BA1=
时,由①AB=1,则BA1=![]() ,则点A1横坐标为
,则点A1横坐标为![]() +
+![]() =2
=2![]() ,B1点纵坐标为
,B1点纵坐标为![]() 2
2![]() =4=22;
=4=22;
当A1(B1)点横坐标为2![]() ,由①A1B1=2,则B1A2=2
,由①A1B1=2,则B1A2=2![]() ;则点A2横坐标为2
;则点A2横坐标为2![]() +2
+2![]() =4
=4![]() ,B2点纵坐标为
,B2点纵坐标为![]() ×4
×4![]() =8=23;
=8=23;
当A2(B2)点横坐标为4![]() ,由①A2B2=4,则B2A3=4
,由①A2B2=4,则B2A3=4![]() ,则点A3横坐标为4
,则点A3横坐标为4![]() +4
+4![]() =8
=8![]() ,B3点纵坐标为
,B3点纵坐标为![]() ×8
×8![]() =16=24;
=16=24;
依稀类推
点B2020的纵坐标为22021
故答案为4,22021.

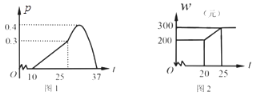
【题目】某农作物的生长率P与温度t(℃)有如下关系:如图1,当10≤t≤25时可近似用函数![]() 刻画;当25≤t≤37时可近似用函数
刻画;当25≤t≤37时可近似用函数![]() 刻画.
刻画.
(1)求h的值.
(2)按照经验,该作物提前上市的天数m(天)与生长率P满足函数关系:
生长率P | 0.2 | 0.25 | 0.3 | 0.35 |
提前上市的天数m(天) | 0 | 5 | 10 | 15 |
①请运用已学的知识,求m关于P的函数表达式;
②请用含![]() 的代数式表示m ;
的代数式表示m ;
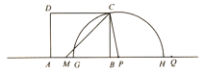
(3)天气寒冷,大棚加温可改变农作物生长速度.在(2)的条件下,原计划大棚恒温20℃时,每天的成本为200元,该作物30天后上市时,根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此给大棚继续加温,加温后每天成本w(元)与大棚温度t(℃)之间的关系如图2.问提前上市多少天时增加的利润最大?并求这个最大利润(农作物上市售出后大棚暂停使用).