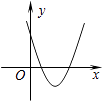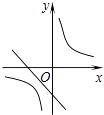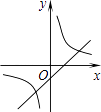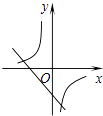题目内容
【题目】阅读下面材料:
小明遇到这样一个问题:
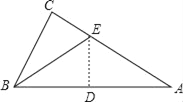
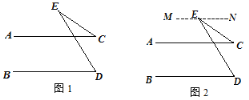
(1)如图1,AC∥BD,点E为直线AC上方一点,连接CE、DE,猜想∠C、∠D、∠E的数量关系,并证明.小明发现,可以过点E作MN∥AC来解决问题,如图2,请你完成解答:
(2)用学过的知识或参考小明的方法,解决下面的问题:
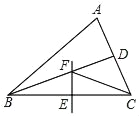
如图3,AB∥CD,P是平面内一点,连接AP、CP,使AP∥BD,∠APC=100°,BM、CM分别平分∠ABD,∠DCP交于点M,求∠M的度数.

【答案】(1)证明见解析;(2)∠CMB=140°.见解析.
【解析】
(1)过点E作MN∥AC, 从而得到MN//AC//BD,再由平行线的性质得到:∠NED=∠D,∠NEC=∠C,从而得到∠D=∠C+∠CED;
(2) 过点M作EF∥CD,过点P作HQ∥CD则EF∥HQ∥CD∥AB,再根据平行线的性质和角平分线的性质得到∠APC=180°-∠CPH-∠APQ,从而求得度数.
(1)证明:过点E作MN∥AC
∵AC∥BD
∴MN∥BD
∴∠NED=∠D
∵MN∥AC
∴∠NEC=∠C
∵∠NED=∠NEC+∠CED
∴∠D=∠C+∠CED;
(2)解:过点M作EF∥CD,过点P作HQ∥CD, 如图:
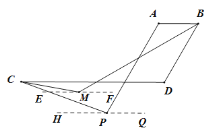
∵AB∥CD
∴EF∥HQ∥CD∥AB.
∵BM、CM分别平分∠ABD,∠DCP
∴设∠ABM=∠MBN=α,∠DCM=∠MCP=β
∵CD∥EF
∴∠DCM=∠CME=β
∵AB∥EF
∴∠ABM=∠BMF=α
∴∠CMB=180°-∠CME-∠BMF=180°-α-β
∵CD∥HQ
∴∠DCP=∠CPH=2α
∵AB∥HQ
∴∠BAP+∠APQ=180°
∵BN∥AP
∴∠BAP+∠ABN=180°
∴∠APQ=∠ABN=2β
∴∠APC=180°-∠CPH-∠APQ=180°-2α-2β=100°
∴α+β=40°
∴∠CMB=180°-α-β=140°.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】某校为了解学生平均每天课外阅读的时间,随机调查了该校部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),将有关数据统计整理并绘制成尚未完成的频率分布表和频数分布直方图.请你根据图表中所提供的信息,解答下列问题.
频率分布表
组别 | 分组 | 频数 | 频率 |
1 | 15~25 | 7 | 0.14 |
2 | 25~35 | a | 0.24 |
3 | 35~45 | 20 | 0.40 |
4 | 45~55 | 6 | b |
5 | 55~65 | 5 | 0.10 |
注:这里的15~25表示大于等于15同时小于25.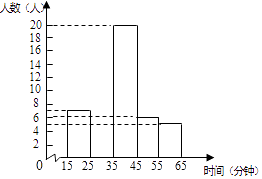
(1)求被调查的学生人数;
(2)直接写出频率分布表中的a和b的值,并补全频数分布直方图;
(3)若该校共有学生500名,则平均每天课外阅读的时间不少于35分钟的学生大约有多少名?
【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.