Question

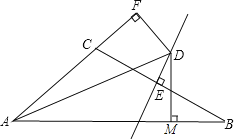
【题目】如图1，已知直线的解析式为，直线的解析式为，且的面积为6.

(1)求和的值.

(2)如图1，将直线绕点逆时针旋转得到直线，点在轴上，若点为轴上的一个动点，点为直线上的一个动点，当的值最小时，求此时点的坐标及的最小值.

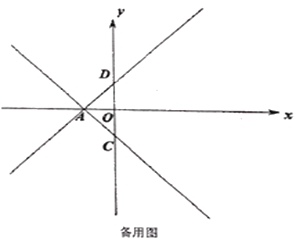
(3)如图2，将沿着直线平移得到，与轴交于点，连接、，当是等腰三角形时，求此时点坐标.

Answer 1

【答案】（1），b=-2，；（2）M(，0)，的最小值为；（3）当是等腰三角形时，P(2,0)或P（6,0）.

【解析】

(1)根据得到点C的坐标，代入得到b=-2，根据的面积为6，求出点B的坐标，代入即可求出k的值；

(2)根据点A、C的坐标求出∠OAC=45，由将直线绕点逆时针旋转得到直线，点在轴上，得到OD=OA=2，过点A作A⊥x轴，且A=AB=6-（-2）=8，连接B，此时点B与点关于直线AD对称，连接C交直线AD于点N，交x轴于点M，此时的值最小，利用勾股定理求出C的长度即可；

(3)根据平移设点的坐标为（c，-c-2），由平移设直线的解析式为y=x+m，利用点求得直线的解析式为y=x-2c-2，得到点P（2c+2,0），利用勾股定理求得、、，分三种情况求出c的值，即可得到点P的坐标.

(1)令中x=0，得y=-2，∴C(0，-2)，∴OC=2，

将点C的坐标代入中，得b=-2，

∴直线AC的解析式为y=-x-2，

∵的面积为6，

∴，

∴OB=6，点B的坐标为（6,0），

将点B的坐标代入中，得6k-2=0，∴；

(2)

∵直线AC的解析式为y=-x-2，

∴当y=0时，x=-2，∴A（-2,0），

∴OA=OC,

∴∠OAC=45，

∵将直线绕点逆时针旋转得到直线，点在轴上，

∴∠OAD=45，

∴OD=OA=2，

过点A作A⊥x轴，且A=AB=6-（-2）=8，连接B，此时点B与点关于直线AD对称，连接C交直线AD于点N，交x轴于点M，此时的值最小.

设直线的解析式为y=dx+e，将点C(0，-2), (-2,8)代入，得

，得，∴直线的解析式为y=-5x-2，

当y=0时，，∴M(，0)，

∵OC=OA=OD，

∴DM=MC，

∵BN=N，

∴

=MC+MN+N，

=C，

过点C作CE⊥A，

∴CE=2，E=10，

∴C=，

∴的最小值为.

(3)设直线AD的解析式为y=ax+n，将点A（-2,0），D(0，2)代入，

∴，得

∴设直线AD的解析式为y=x+2，

由(2)知：直线AC的解析式为y=-x-2，

设点的坐标为（c，-c-2），

由平移设直线的解析式为y=x+m，将点的坐标代入，得

c+m=-c-2，

m=-2c-2，

∴直线的解析式为y=x-2c-2，

当y=0时，x=2c+2，∴P（2c+2,0），

过点作H⊥x轴于H，作E⊥y轴于E，

∴=2c+2-c=c+2， =c+2，E=c，DE=2-(-c-2)=c+4，

∴，

，

,

当是等腰三角形时，分三种情况：

①当P=D时，得，方程无解，舍去；

②当P=PD时，得，得c=0，

∴P(2,0)，

③当D=PD时，得，得c=2或,c=-2（舍去），

∴P（6,0），

综上，当是等腰三角形时，P(2,0)或P（6,0）.