题目内容
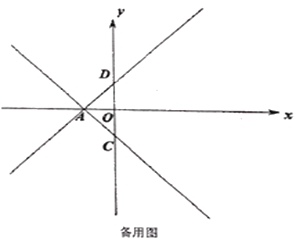
【题目】如图,四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC.
求证:
(1)CD⊥DF;
(2)BC=2CD.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)利用在同圆中所对的弧相等,弦相等,所对的圆周角相等,三角形内角和可证得∠CDF=90°,则CD⊥DF;
(2)应先找到BC的一半,证明BC的一半和CD相等即可.
证明:(1)∵AB=AD,
∴弧AB=弧AD,∠ADB=∠ABD.
∵∠ACB=∠ADB,∠ACD=∠ABD,
∴∠ACB=∠ADB=∠ABD=∠ACD.
∴∠ADB=(180°﹣∠BAD)÷2=90°﹣∠DFC.
∴∠ADB+∠DFC=90°,即∠ACD+∠DFC=90°,
∴CD⊥DF.
(2)过F作FG⊥BC于点G,
∵∠ACB=∠ADB,
又∵∠BFC=∠BAD,
∴∠FBC=∠ABD=∠ADB=∠ACB.
∴FB=FC.
∴FG平分BC,G为BC中点,![]()
∵在△FGC和△DFC中,
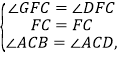
∴△FGC≌△DFC(ASA),
∴![]()
∴BC=2CD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】小明选择一家酒店订春节团圆饭.他借助网络评价,选择了A、B、C三家酒店,对每家酒店随机选择1000条网络评价统计如下:
评价条数 等级 酒店 | 五星 | 四星 | 三星及三星以下 | 合计 |
A | 412 | 388 |
| 1000 |
B | 420 | 390 | 190 | 1000 |
C | 405 | 375 | 220 | 1000 |
(1)求x值.
(2)当客户给出评价不低于四星时,称客户获得良好用餐体验.
①请你为小明从A、B、C中推荐一家酒店,使得能获得良好用餐体验可能性最大.写出你推荐的结果,并说明理由.
②如果小明选择了你推荐的酒店,是否一定能够享受到良好用餐体验?