题目内容
【题目】已知AB是⊙O的直径,点P是直径AB上任意一点,过点P作弦CD⊥AB,垂足为点P,过B点的直线与线段AD的延长线交于点F,且∠F=∠ABC.
(1)如图1,求证:直线BF是⊙O的切线;
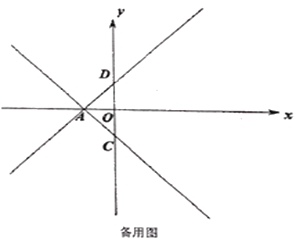
(2)如图2,当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?证明你的结论.

【答案】(1)详见解析;(2)四边形![]() 是平行四边形,证明详见解析.
是平行四边形,证明详见解析.
【解析】
(1)欲证明直线BF是⊙O的切线,只要证明∠ABF=90°.
(2)结论四边形AEBF是平行四边形,只要证明AE∥BF,AF∥BE即可.
(1)如图1中,∵∠A=∠C,∠F=∠ABC,∴∠ABF=∠CPB.
∵CD⊥AB,∴∠CPB=90°,∴∠ABF=90°,∴直线BF是⊙O的切线.
(2)结论:四边形AEBF是平行四边形.证明如下:
如图2中,连接AC、BD.
∵OA=OB,∴OC=OD,∴四边形ACBD是平行四边形,∴AD∥BC,即AF∥BE.
又∵AE切⊙O于点A,∴AE⊥AB,同理BF⊥AB,∴AE∥BF,∴四边形AEBF是平行四边形.

练习册系列答案
相关题目