Question

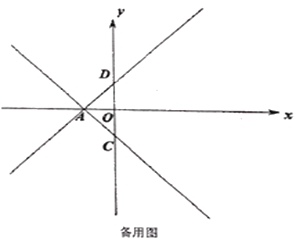
【题目】在数学上，我们把符合一定条件的动点所形成的图形叫做满足该条件的点的轨迹．例如：动点P的坐标满足（m，m﹣1），所有符合该条件的点组成的图象在平面直角坐标系xOy中就是一次函数y=x﹣1的图象．即点P的轨迹就是直线y=x﹣1．

（1）若m、n满足等式mn﹣m=6，则（m，n﹣1）在平面直角坐标系xOy中的轨迹是　 　；

（2）若点P（x，y）到点A（0，1）的距离与到直线y=﹣1的距离相等，求点P的轨迹；

（3）若抛物线y=上有两动点M、N满足MN=a（a为常数，且a≥4），设线段MN的中点为Q，求点Q到x轴的最短距离．

Answer 1

【答案】（1）；（2）y=x2；（3）点Q到x轴的最短距离为1．

【解析】

（1）先判断出m（n﹣1）=6，进而得出结论；

（2）先求出点P到点A的距离和点P到直线y=﹣1的距离建立方程即可得出结论；

（3）设出点M，N的坐标，进而得出点Q的坐标，利用MN=a，得出，即可得出结论．

（1）设m=x，n﹣1=y，

∵mn﹣m=6，

∴m（n﹣1）=6，

∴xy=6，

∴

∴（m，n﹣1）在平面直角坐标系xOy中的轨迹是

故答案为：；

（2）∴点P（x，y）到点A（0，1），

∴点P（x，y）到点A（0，1）的距离的平方为x2+（y﹣1）2，

∵点P（x，y）到直线y=﹣1的距离的平方为（y+1）2，

∵点P（x，y）到点A（0，1）的距离与到直线y=﹣1的距离相等，

∴x2+（y﹣1）2=（y+1）2，

∴

（3）设直线MN的解析式为y=kx+b，M（x1，y1），N（x2，y2），

∴线段MN的中点为Q的纵坐标为

∴

∴x2﹣4kx﹣4b=0，

∴x1+x2=4k，x1x2=﹣4b，

∴

∴

∴

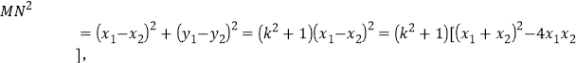
∴点Q到x轴的最短距离为1．