题目内容
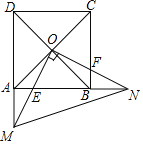
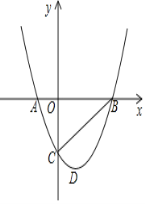
【题目】如图,在直角坐标系中,点![]() 在第一象限,
在第一象限,![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,![]() ,
,![]() ,有一反比例函数图象刚好过点
,有一反比例函数图象刚好过点![]() .
.

(1)分别求出过点![]() 的反比例函数和过
的反比例函数和过![]() ,
,![]() 两点的一次函数的函数表达式;
两点的一次函数的函数表达式;
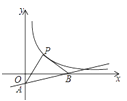
(2)直线![]() 轴,并从
轴,并从![]() 轴出发,以每秒
轴出发,以每秒![]() 个单位长度的速度向
个单位长度的速度向![]() 轴正方向运动,交反比例函数图象于点
轴正方向运动,交反比例函数图象于点![]() ,交
,交![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,当直线
,当直线![]() 运动到经过点
运动到经过点![]() 时,停止运动.设运动时间为
时,停止运动.设运动时间为![]() (秒).
(秒).
①问:是否存在![]() 的值,使四边形
的值,使四边形![]() 为平行四边形?若存在,求出
为平行四边形?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
②若直线![]() 从
从![]() 轴出发的同时,有一动点
轴出发的同时,有一动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向,以每秒
方向,以每秒![]() 个单位长度的速度运动.是否存在
个单位长度的速度运动.是否存在![]() 的值,使以点
的值,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形;若存在,求出
为顶点的四边形为平行四边形;若存在,求出![]() 的值,并进一步探究此时的四边形是否为特殊的平行四边形;若不存在,说明理由.
的值,并进一步探究此时的四边形是否为特殊的平行四边形;若不存在,说明理由.
【答案】(1)![]() ,
, ![]() ;(2)①不存在,理由详见解析;②存在,
;(2)①不存在,理由详见解析;②存在,![]()
【解析】
(1)先确定A、B、C的坐标,然后用待定系数法解答即可;
(2)①可用t的代数式表示DF,然后根据DF=BC求出t的值,得到DF与CB重合,因而不存在t,使得四边形DFBC为平行四边形;②可分两种情况(点Q在线段BC上和在线段BC的延长线上)讨论,由于DE∥QC,要使以点D、E、Q、C为顶点的四边形为平行四边形,只需DE=QC,只需将DE、QC分别用的式子表示,再求出t即可解答.
解:(1)由题意得![]() ,
,![]() ,
,![]() ,
,
![]() 反比例函数为
反比例函数为![]() ,一次函数为:
,一次函数为:![]() .
.
(2)①不存在.
![]() 轴,
轴,![]() 轴,
轴,
![]() .
.
又![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() .
.
设![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
此时![]() 与
与![]() 重合,不符合题意,
重合,不符合题意,
![]() 不存在.
不存在.
②存在.当![]() 时,
时,![]() ;当
;当![]() 时,由
时,由![]() ,
,![]() ,得
,得![]() .
.
由![]() ,
,![]() .得
.得![]() .
.
![]()
![]() 当
当![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.
![]() .
.
![]() ,
,
![]() (舍)
(舍)
![]() 当
当![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.
又![]() 且
且![]() ,
,
![]() 为矩形.
为矩形.

练习册系列答案
相关题目