题目内容
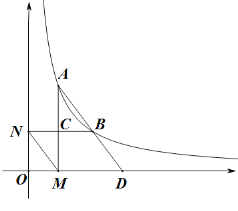
【题目】如图,已知反比例函数y=![]() (x>0,k是常数)的图象经过点A(1,4),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
(x>0,k是常数)的图象经过点A(1,4),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
(1)求出反比例函数解析式;
(2)求证:△ACB∽△NOM.
(3)延长线段AB,交x轴于点D,若点B恰好为AD的中点,求此时点B的坐标.
【答案】(1)![]() (2)详见解析;(3)B(2,2)
(2)详见解析;(3)B(2,2)
【解析】
(1)将点A的坐标代入反比例函数y=![]() (x>0,k是常数)中,即可求得;
(x>0,k是常数)中,即可求得;
(2)由于∠ACB =∠NOM = 90°,所以要证ΔACB∽ΔNOM,只要![]() 即可,由已知分别求出
即可,由已知分别求出![]() 和
和![]() ,证明它们相等即可;
,证明它们相等即可;
(3)由AM⊥x轴求得AM=4,由BN//OD可得,点C是AM的中点,则CM=2,则点B的纵坐标为2,从而求得点B横坐标.
(1)∵反比例函数y=![]() (x>0,k是常数)的图象经过点A(1,4),
(x>0,k是常数)的图象经过点A(1,4),
∴k=xy=4,
∴反比例函数解析式:y=![]() (x>0);
(x>0);
(2) ∵ B(m,n),A(1,4),∴AC = 4–n,BC = m–1,ON = n,OM = 1.
∴![]() =
=![]() .
.
∵点B(m,n)在y=![]() 上,
上,
∴m=![]() .
.
∴![]() =m-1.
=m-1.
又∵![]() .
.
∴![]() .
.
又∵∠ACB =∠NOM = 90°,
∴ ΔACB∽ΔNOM.
(3) ∵AM⊥x轴,且A(1,4),
∴点C的横坐标1,AM=4,
∵BN//x轴,点B是AD的中点,
∴点C是AM的中点,
∴CM=2,即点B的纵坐标为2,
又∵点B在反比例函数y=![]() 上,
上,
∴点B纵坐标为2,
∴点B的坐标为(2,2).

【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.