题目内容
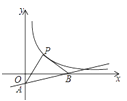
【题目】如图,直线y=![]() x﹣1与坐标轴交于A,B两点,点P是曲线y=
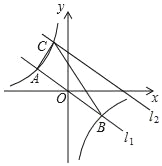
x﹣1与坐标轴交于A,B两点,点P是曲线y=![]() (x>0)上一点,若△PAB是以∠APB=90°的等腰三角形,则k= _________.
(x>0)上一点,若△PAB是以∠APB=90°的等腰三角形,则k= _________.
【答案】4
【解析】
根据全等三角形的判定与性质,可得AD=BC,DP=CP,根据AD=BC,可得关于x的方程,根据解方程,可得x,根据待定系数法,可得函数解析式.
解:作PC⊥x轴,PD⊥y轴,如图 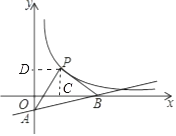 ,
,
∴∠COD=∠ODM=∠OCM=90°,
∴四边形OCPD是矩形.
在△APD和△BPC中, ,
,
∴△APD≌△BPC(AAS),
∴AD=BC,DP=CP,
∴四边形OCPD是正方形,
∴OC=OD,
∵OA=1,OB=5,
设OD=x,
则AD=x+1,BC=5﹣x,
∵AD=BC,
∴x+1=5﹣x,
解得:x=2,
即OD=OC=2,
∴点P的坐标为:(2,2),
∴k=xy=4,
故答案为:4.

练习册系列答案
相关题目