题目内容
【题目】若反比例函数y＝
与一次函数y＝2x－4的图象都经过点A(a，2)．
(1)求反比例函数y＝的表达式；
(2)当反比例函数y＝的值大于一次函数y＝2x－4的值时，求自变量x的取值范围．
【答案】（1）y=
；（2）x＜-1或0＜x＜3．
【解析】
（1）将A坐标代入一次函数解析式求出a的值，确定出A坐标，将A坐标代入反比例解析式求出k的值，即可确定出反比例解析式；
（2）联立两函数解析式求出交点坐标，画出两函数图象，利用图象即可得出满足题意x的范围．
（1）将A（a，2）代入一次函数y=2x-4中得：2=2a-4，即a=3，
∴A（3，2），
将x=3，y=2代入反比例解析式得：k=6，
则反比例解析式为y=；
（2）联立两函数解析式得：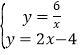
，
解得：
或
，
即两函数的两交点分别为（3，2），（-1，-6），作出两函数图象，如图所示：
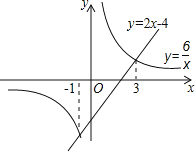
则由函数图象得：反比例函数y=的值大于一次函数y=2x-4的值时，自变量x的取值范围为x＜-1或0＜x＜3．
练习册系列答案
相关题目
