��Ŀ����
����Ŀ����ͼ��ƽ��ֱ������ϵ�У����κ���y=x2��2x��3�IJ���ͼ����x�ύ�ڵ�A��
B��A��B����ߣ�����y�ύ�ڵ�C������BC��DΪ���㣮
��1������OBC�Ķ�����
��2����x���·������������Ƿ����һ��Q��ʹ��ABQ���������5������ڣ���Q������꣬�粻���ڣ�˵�����ɣ�
��3����P�ǵ��������������ϵ�һ�����㣨�����D�غϣ�������P��PF��x�ύBC�ڵ�F�����߶�PF���ȵ����ֵ��
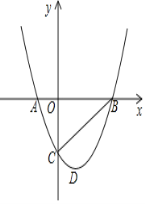
���𰸡���1����OBC=45�㣻��2����Q������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ������3��PF�����ֵ��
������3��PF�����ֵ��![]() ��
��
��������
��1������������֪�������������OBC�ĸ������㣬��֪��������״���ڽǣ�
��2����Ϊ�������ѹ̶����������Q��AB�ľ���Ϊa�Լ���ABQ���������5�����a��ֵ��Ȼ�������κ����ı���ʽ���������Q�����ꣻ
��3��PF�ij��ȼ�ΪyF-yP����P��F�ĺ�������ͬ�����ֱ�����ý���ʽ��������ú���Ϊ���κ���������ö��κ�������������ֵ���ⷨ���森
��1����y=x2-2x-3=��x-3����x+1����
�൱x=0ʱ��y=-3����y=0ʱ��x=-1��x=3��
���C��������0��-3������B��3��0������A��-1��0����
��OC=3��OB=3��
��OB=OC��
���OBC=��OCB��
�ߡ�BOC=90����
���OBC=��OCB=45����
����OBC=45����
��2����x���·����������ϴ���һ��Q��ʹ��ABQ���������5��
�ߵ�B��3��0������A��-1��0����
��AB=4��
���Q��AB�ľ���Ϊa��
�ߡ�ABQ���������5��
��![]() =5����a=
=5����a=![]() ��
��
�ߵ�Q��x���·���
���Q����������-![]() ��
��
��y=-![]() ����y=x2-2x-3����
����y=x2-2x-3����
-![]() =x2-2x-3��
=x2-2x-3��
��ã�x=![]() ��
��
���Q��������![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��3��
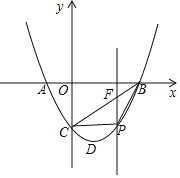
�����C��0��-3���͵�B��3��0����ֱ�߽���ʽΪy=kx+b��
![]() ����
����![]() ��
��
��ֱ��BC�ĺ�������ʽΪy=x-3��
���P��������m��m2-2m-3����
��x=m����y=x-3����y=m-3��
���F��������m��m-3����
��PF=m-3-��m2-2m-3��=-m2+3m=-��m-![]() ��2+
��2+![]() ��
��
�൱m=![]() ʱ��PFȡ�����ֵ����ʱPF=
ʱ��PFȡ�����ֵ����ʱPF=![]() ��
��
��PF�����ֵ��![]() ��
��