题目内容
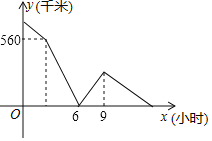
【题目】A、B、C三地在同一直线上，甲、乙两车分别从A，B两地相向匀速行驶，甲车先出发2小时，甲车到达B地后立即调头，并将速度提高10%后与乙车同向行驶，乙车到达A地后，继续保持原速向远离B的方向行驶，经过一段时间后两车同时到达C地，设两车之间的距离为y（千米），甲行驶的时间x（小时）．y与x的关系如图所示，则B、C两地相距_____千米．
【答案】1320．
【解析】
根据题意和函数图象中的数据，可以求得甲乙两车的速度，再根据“路程=速度×时间”，即可解答本题．
解：设甲车的速度为a千米/小时，乙车的速度为b千米/小时，
，解得
，
∴A、B两地的距离为：80×9＝720千米，
设乙车从B地到C地用的时间为x小时，
60x＝80（1+10%）（x+2﹣9），
解得，x＝22，
则B、C两地相距：60×22＝1320（千米）
故答案为：1320．
练习册系列答案
口算题天天练系列答案
相关题目
