题目内容
【题目】在
中，
，
，点
是
上的一点，连接
，作
交
于点
．
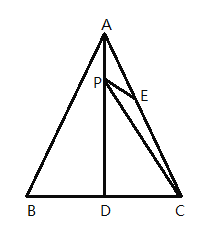
（1）如图1，当
时，求证：
；
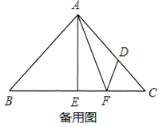
（2）如图2，作
于点
，当
时，求证：
；
（3）在（2）的条件下，若
，求
的值．
【答案】（1）见解析；（2）见解析；（3）32．
【解析】
（1）利用三角形外角的性质证得
，从而证得
，即可证明结论；
（2）利用三角形外角的性质证得
，继而求得
，从而证得结论；
（3）作出如图辅助线，利用
证得
，利用等腰三角形三线合一的性质求得
，用面积法求得
，从而证得结论．
（1）∵
，
∴
，
∵
，
，
，
∴，
∵
，
∴，
∴
，
∵，
∴
；
（2）∵，
，
∴
，
∵，，，
∴，
∵
，
∴，
∵
，
∴
，
∵
，
∴，
∵，
，
∴
，
∵，
∴
，
∴
，
∵
，
∴
；
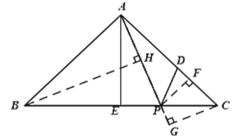
（3）过点
作
交
延长线于点
，过点
作
于点
，过点
作
于点
，
∴
，
∵
，
，
∴
，
∵，
∴，
∴，
∵
，
，
∴
，
∴
，
∵，
∴
，
∵
，
∴
，
∴，
∴
，
∵
，
∴，
∵
，，
∴
，
∵，
∴
，
∴
练习册系列答案
相关题目
【题目】某公司实行年工资制，职工的年工资由基础工资、住房补贴和医疗费三项组成，具体规定如下：
项目 | 第一年的工资（万元） | 一年后的计算方法 |
基础工资 | 1 | 每年的增长率相同 |
住房补贴 | 0.04 | 每年增加0.04 |
医疗费 | 0.1384 | 固定不变 |
（1）设基础工资每年增长率为x，用含x的代数式表示第三年的基础工资为 万元；
（2）某人在公司工作了3年，他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %，问基础工资每年的增长率是多少？
【题目】甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图:
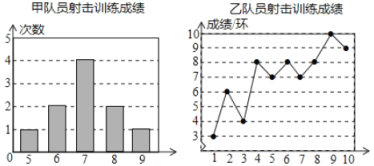
根据以上信息，整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)
_ ；
；
；
(2)填空:(填“甲”或“乙”)，
①从平均数和中位数的角度来比较，成绩较好的是 ；
②从平均数和众数的角度来比较，成绩较好的是 ；
③成绩相对较稳定的是 ；
(3)若
环以上有希望夺冠，选派其中一名参赛，你认为应选 队员.
