题目内容
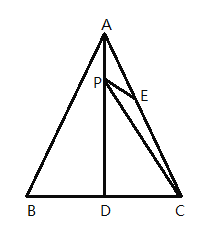
【题目】如图,△ABC中, AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且AE=AB.
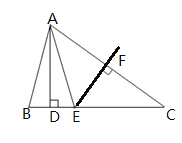
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC周长26cm,AC=10cm,求DC长.
【答案】(1)∠C=35°;(2)8cm
【解析】
(1)根据线段垂直平分线和等腰三角形性质得出AB=AE=CE,即可求出∠AEB,由∠C=∠EAC,即可得出答案;
(2)根据题意,有AB=CE,BD=DE,能推出2DE+2EC=16cm,即可得出答案.
解:(1)∵AD⊥BC,AE=AB,EF垂直平分AC,
∴AB=AE=EC,
∴∠C=∠CAE,
∵∠BAE=40°,
∴∠AED=![]() ,
,
∴∠C=![]() ∠AED=35°;
∠AED=35°;
(2)∵△ABC周长26cm,AC=10cm,
∴AB+BC=![]() cm,
cm,
∴AB+BE+EC=16cm,
∵AB=CE,BD=DE,
∴2DE+2EC=16cm,
∴DE+EC=8cm,
∴DC=DE+EC=8cm.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
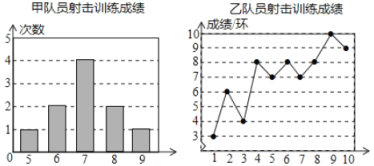
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)![]() _ ;
_ ;![]() ;
;![]() ;
;
(2)填空:(填“甲”或“乙”),
①从平均数和中位数的角度来比较,成绩较好的是 ;
②从平均数和众数的角度来比较,成绩较好的是 ;
③成绩相对较稳定的是 ;
(3)若![]() 环以上有希望夺冠,选派其中一名参赛,你认为应选 队员.
环以上有希望夺冠,选派其中一名参赛,你认为应选 队员.
【题目】某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:
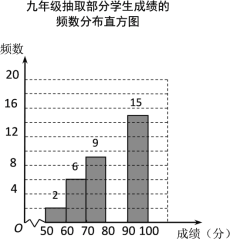
![]()
成绩x/分 | 频数 | 频率 | |
第1段 | x<60 | 2 | 0.04 |
第2段 | 60≤x<70 | 6 | 0.12 |
第3段 | 70≤x<80 | 9 | b |
第4段 | 80≤x<90 | a | 0.36 |
第5段 | 90≤x≤100 | 15 | 0.30 |
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)样本中,部分学生成绩的中位数落在第_______段;
(4)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?