题目内容
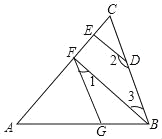
【题目】如图,在ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.

【答案】(1)详见解析;(2)13.
【解析】
(1)只要证明DN∥BM,DM∥BN即可;
(2)只要证明△CEM≌△AFN,可得FN=EM=5,在Rt△AFN中,根据勾股定理AN=![]() 即可解决问题;
即可解决问题;
(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,
∵BM⊥AC,DN⊥AC,
∴DN∥BM,
∴四边形BMDN是平行四边形;
(2)∵四边形BMDN是平行四边形,
∴DM=BN,
∵CD=AB,CD∥AB,
∴CM=AN,∠MCE=∠NAF,
∵∠CEM=∠AFN=90°,
∴△CEM≌△AFN,
∴FN=EM=5,
在Rt△AFN中,AN=![]() =
=![]() =13.
=13.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目