题目内容
【题目】在△ABC 中,∠ACB=90° AD 是它的角平分线,EB⊥AB 于点 B 且交 AD 的延长线于点 E.
(1)如图 1,求证:BD=BE
(2)如图 2,过点 E 作 EF⊥BC 于点 F, CF:BF=5:3, BE=10,求 DF 的长.
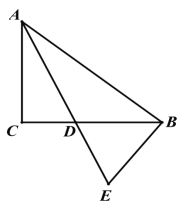
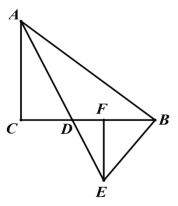
图 1 图 2
【答案】(1)证明见解析.(2)DF=4
【解析】分析: (1)过点B作BG⊥DE于G, 根据AD是△ABC的角平分线, EB⊥AB得∠ADC=∠E, 再证∠BGD=∠BGE,最后根据BG=BG可证△BDG≌△BEG,从而可得BD=BE.
(2)过点D作DH⊥AB于H,先证△BHD≌△EBF,得到 DH=BF,从而CD=BF.设CF=5x,BF=3x,根据BD=BF+DF可求出x的值,可求出DF的值.
详解:
(1)证明:过点B作BG⊥DE于G
∵AD是△ABC的角平分线
∴∠BAD=∠CAD
∵EB⊥AB
∴∠ABE=90°
在Rt△ABE中
∠BAE+∠E=90°
在Rt△ACD中
∠CAD+∠ADC=90°
∴∠ADC=∠E
∵∠ADC=∠BDE
∴∠BDE=∠E
∵BG⊥DE
∴∠BGD=∠BGE
∵BG=BG
∴△BDG≌△BEG(AAS)
∴BD=BE
(2)过点D作DH⊥AB于H,
∵ ∠ACB=90°
∴ CD⊥AC
∴ CD=DH
∵ ∠ABE=90°
∴ ∠ABC+∠FBE=90
∵ EF⊥BD
∴ ∠BFE=90°
∴ ∠FEB+∠FBE=90°
∴ ∠HBD=∠FEB
∵ DH⊥AB
∴ ∠BHD=90°
∴ △BHD≌△EBF(AAS)
∴ DH=BF
∴ CD=BF
∵ CF:BF=5:3
∵ 设CF=5x,BF=3x,则CD=3x,
DF=CF-CD=5x-3x=2x
BD=BF+DF=3x+2x==5x
∵ BE=10
∴ 5x=10,x=2
∴ DF=2×2=4

 名校课堂系列答案
名校课堂系列答案