Question

【题目】已知AP是△ABC的外角平分线，连结PB、PC．

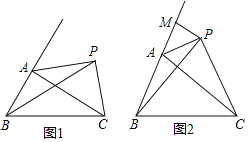
（1）如图1①若BP平分∠ABC，且∠ACB＝28°，求∠APB的度数．

②若P与A不重合，请判断AB+AC与PB+PC的大小关系，并证明你的结论．

（2）如图2，若过点P作PM⊥BA，交BA的延长线于M点，且∠BPC＝∠BAC，求：的值．

Answer 1

【答案】（1）①14°；②PB+PC＞AB+AC，证明见解析；（2）

【解析】

（1）根据三角形的角平分线的定义和三角形外角的性质即可得到结论；

（2）在射线AD上取一点H，是的AH＝AC，连接PH．则△APH≌△APC，根据三角形的三边关系即可得到结论．

（3）过P作PN⊥AC于N，根据角平分线的性质得到PM＝PN，根据全等三角形的性质得到AM＝AN，BM＝CN，于是得到结论．

解：（1）①∵AP平分∠DAC，PB平分∠ABC，

∴∠DAP＝∠DAC，∠ABP＝∠ABC，

∵∠DAC＝∠ABC+∠ACB，∠DAP＝∠ABP+∠APB，

∴∠APB＝∠DAP﹣∠ABP＝∠DAC﹣∠ABC＝∠ACB＝14°；

②PB+PC＞AB+AC．

理由如下：

如图1﹣1，在射线AD上取一点H，使AH＝AC，连接PH．

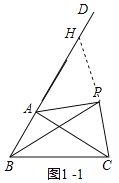
∵AC＝AH，∠PAD＝∠PAC，AP＝AP，

∴△APH≌△APC（SAS），

∴PC＝PH，

在△BPH中，PB+PH＞BH，

∴PB+PC＞AB+AC．

（2）过点P作PN⊥AC于N，

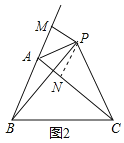
∵AP平分∠MAN，PM⊥BA，

∴PM＝PN，

在Rt△APM与Rt△APN中，

，

∴Rt△APM≌Rt△APN（HL），

∴AM＝AN，

∵∠BAC＝∠BPC，

∴由“8字形”得：∠MBP＝∠PCN，

在△PMB与△PNC中，

，

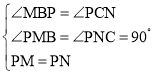∴△PMB≌△PNC（AAS）

∴BM＝CN，

∵AM＝AN，

∴AC﹣AB＝2AM，

∴＝＝