题目内容
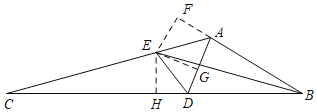
【题目】如图,在△ABD中,∠BAD=80°,C为BD延长线上一点,∠BAC=130°,∠ABD的角平分线与AC交于点E,连接DE.

(1)求证:点E到DA、DC的距离相等;
(2)求∠BED的度数.
【答案】(1)见解析;(2)∠BED=40°
【解析】
(1)作辅助线,构建角平分线的距离,根据角平分线的性质和逆定理可得:EF=EG=EH,进而解答即可;
(2)设∠DEG=y,∠GEB=x,根据三角形的内角和定理可得:∠GEA=∠FEA=40°,∠FEB=∠HEB,列方程为2y+x=80﹣x,y+x=40,可得结论:∠DEB=40°.
证明:(1)过E作EF⊥AB于F,EG⊥AD于G,EH⊥BC于H,
∵BE平分∠ABD,
∴EH=EF,
∵∠BAC=130°,
∴∠FAE=∠CAD=50°,
∴EF=EG,
∴EG=EH,
∴ED平分∠CDG,
∴点E到DA、DC的距离相等;
(2)∵ED平分∠CDG,
∴∠HED=∠DEG,
设∠DEG=y,∠GEB=x,
∵∠EFA=∠EGA=90°,
∴∠GEA=∠FEA=40°,
∵∠EFB=∠EHB=90°,∠EBF=∠EBH,
∴∠FEB=∠HEB,
∴2y+x=80﹣x,
2y+2x=80,
y+x=40,
即∠DEB=40°.

练习册系列答案
相关题目