ΧβΡΩΡΎ»ί
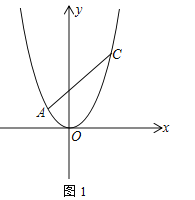
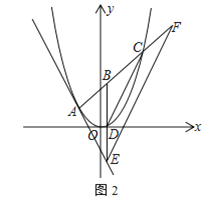
ΓΨΧβΡΩΓΩ“―÷ΣΕΰ¥ΈΚ· ΐy1ΘΫx2+mx+nΒΡΆΦœσΨ≠ΙΐΒψPΘ®©¹3Θ§1Θ©Θ§Ε‘≥Τ÷α «Ψ≠ΙΐΘ®©¹1Θ§0Θ©«“ΤΫ––”Ύy÷αΒΡ÷±œΏΘ°
Θ®1Θ©«σmΘ§nΒΡ÷ΒΘ§
Θ®2Θ©»γΆΦΘ§“Μ¥ΈΚ· ΐy2ΘΫkx+bΒΡΆΦœσΨ≠ΙΐΒψPΘ§”κx÷αœύΫΜ”ΎΒψAΘ§”κΕΰ¥ΈΚ· ΐΒΡΆΦœσœύΫΜ”ΎΝμ“ΜΒψBΘ§»τΒψB”κΒψMΘ®©¹4Θ§6Θ©ΙΊ”Ύ≈ΉΈοœΏΕ‘≥Τ÷αΕ‘≥ΤΘ§«σ“Μ¥ΈΚ· ΐΒΡ±μ¥ο ΫΘ°
Θ®3Θ©ΗυΨίΚ· ΐΆΦœσ÷±Ϋ”–¥≥ωy1ΘΨy2 ±xΒΡ»Γ÷ΒΖΕΈßΘ°
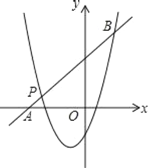
ΓΨ¥πΑΗΓΩΘ®1Θ©2Θ§![]() ΘΜΘ®2Θ©yΘΫx+4ΘΜΘ®3Θ©xΘΦ©¹3ΜρxΘΨ2.
ΘΜΘ®2Θ©yΘΫx+4ΘΜΘ®3Θ©xΘΦ©¹3ΜρxΘΨ2.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΫΪΒψPΘ®-3Θ§1Θ©¥ζ»κΕΰ¥ΈΚ· ΐΫβΈω ΫΒΟ≥ω3m©¹nΘΫ8Θ§»ΜΚσΗυΨίΕ‘≥Τ÷αΙΐΒψΘ®-1Θ§0Θ©ΒΟ≥ωΕ‘≥Τ÷αΈΣx=-1Θ§Ψί¥Υ«σ≥ωmΒΡ÷ΒΘ§»ΜΚσΫχ“Μ≤Ϋ«σ≥ωnΒΡ÷ΒΦ¥Ω…ΘΜ
Θ®2Θ©ΗυΨί“Μ¥ΈΚ· ΐΨ≠ΙΐΒψPΘ®©¹3Θ§1Θ©Θ§ΒΟ≥ω1ΘΫ©¹3k+bΘ§«“ΒψB”κΒψMΘ®©¹4Θ§6Θ©ΙΊ”ΎxΘΫ©¹1Ε‘≥ΤΘ§Υυ“‘BΘ®2Θ§6Θ©Θ§Υυ“‘6ΘΫ2k+bΘ§ΉνΚσ«σ≥ωk”κbΒΡ÷ΒΦ¥Ω…ΘΜ
Θ®3Θ©y1ΘΨy2Θ§‘ρΥΒΟς y1ΒΡΚ· ΐΆΦœώ‘Ύy2Κ· ΐΆΦœώ…œΖΫΘ§Ψί¥ΥΗυΨίΆΦœώ÷±Ϋ”–¥≥ωΖΕΈßΦ¥Ω….
Θ®1Θ©”…Εΰ¥ΈΚ· ΐΨ≠ΙΐΒψPΘ®©¹3Θ§1Θ©Θ§
Γύ1ΘΫ9©¹3m+nΘ§
Γύ3m©¹nΘΫ8Θ§
”÷ΓΏΕ‘≥Τ÷α «Ψ≠ΙΐΘ®©¹1Θ§0Θ©«“ΤΫ––”Ύy÷αΒΡ÷±œΏΘ§
ΓύΕ‘≥Τ÷αΈΣxΘΫ©¹1Θ§
Γύ©¹![]() ΘΫ©¹1Θ§
ΘΫ©¹1Θ§
ΓύmΘΫ2Θ§
ΓύnΘΫ©¹2ΘΜ
Θ®2Θ©ΓΏ“Μ¥ΈΚ· ΐΨ≠ΙΐΒψPΘ®©¹3Θ§1Θ©Θ§
Γύ1ΘΫ©¹3k+bΘ§
ΓΏΒψB”κΒψMΘ®©¹4Θ§6Θ©ΙΊ”ΎxΘΫ©¹1Ε‘≥ΤΘ§
ΓύBΘ®2Θ§6Θ©Θ§
Γύ6ΘΫ2k+bΘ§
ΓύkΘΫ1Θ§bΘΫ4Θ§
Γύ“Μ¥ΈΚ· ΐΫβΈω ΫΈΣyΘΫx+4ΘΜ
Θ®3Θ©”…ΆΦœσΩ…÷ΣΘ§xΘΦ©¹3ΜρxΘΨ2 ±Θ§y1ΘΨy2Θ°

 ―τΙβΩΈΧΟΩΈ ±”≈Μ·Ής“ΒœΒΝ–¥πΑΗ
―τΙβΩΈΧΟΩΈ ±”≈Μ·Ής“ΒœΒΝ–¥πΑΗ