题目内容
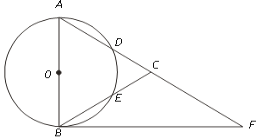
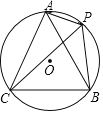
【题目】如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:PA+PB=PC;
(2)若BC=![]() ,点P是劣弧AB上一动点(异于A、B),PA、PB是关于x的一元二次方程x2﹣mx+n=0的两根,求m的最大值.
,点P是劣弧AB上一动点(异于A、B),PA、PB是关于x的一元二次方程x2﹣mx+n=0的两根,求m的最大值.
【答案】(1)详见解析;(2)m的最大值为4.
【解析】
(1)在PC上截取PD=AP,则△APD是等边三角形,然后证明△APB≌△ADC,证明BP=CD,即可证得;
(2)根据一元二次方程的根解答即可.
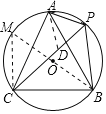
证明:(1)在PC上截取PD=AP,如图,
又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
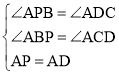 ,
,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP
(2)由(1)可知PA+PB=PC,
∵PA、PB是方程的两根,
∴PA+PB=m,
要使m有最大值,则PA+PB最大,即PC为⊙O的直径,连BO并延长交⊙O于点M,连接CM,
则∠BCM=90°,
∴BMC=∠BPC=60°,
∵BC=2![]() ,
,
∴BG=4,
∴m的最大值为4.

练习册系列答案
相关题目