Question

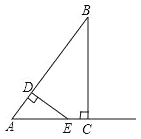
【题目】（2011贵州安顺，16，4分）如图，在Rt△ABC中，∠C=90°，BC=6cm，AC=8cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB边的C′点，那么△ADC′的面积是 ．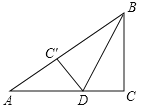

Answer 1

【答案】6cm2

【解析】

先根据勾股定理得到AB=10cm，再根据折叠的性质得到DC=DC′，BC=BC′=6cm，则AC′=4cm，设DC=xcm，在Rt△ADC′中根据勾股定理列方程求得x的值，然后根据三角形的面积公式计算即可．

∵∠C=90°，BC=6cm，AC=8cm，

∴AB=10cm，

∵将△BCD沿BD折叠，使点C落在AB边的C′点，

∴△BCD≌△BC′D，

∴∠C=∠BC′D=90°，DC=DC′，BC=BC′=6cm，

∴AC′=AB-BC′=4cm，

设DC=xcm，则AD=（8-x）cm，

在Rt△ADC′中，AD2=AC′2+C′D2，

即（8-x）2=x2+42，解得x=3，

∵∠AC′D=90°，

∴△ADC′的面积═×AC′×C′D=×4×3=6（cm2）．