题目内容
14.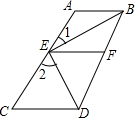 已知:如图,AB∥CD,EF∥AB,BE、DE分别平分∠ABD、∠BDC,若∠1=32°.求∠2的度数.
已知:如图,AB∥CD,EF∥AB,BE、DE分别平分∠ABD、∠BDC,若∠1=32°.求∠2的度数.
分析 先根据AB∥CD得出∠ABD+∠BDC=180°,再根据BE、DE分别平分∠ABD、∠BDC可知∠EBD+∠EDB=90°,由三角形内角和定理可知,∠BED=90°,再根据平角的定义即可得出结论.
解答 解:∵AB∥CD,
∴∠ABD+∠BDC=180°,
∵BE、DE分别平分∠ABD、∠BDC,
∴∠EBD+∠EDB=90°,
∴∠BED=90°,
∴∠1+∠2=90°.
∵∠1=32°.
∴∠2=58°.
点评 本题考查的是平行线的性质,关键是根据两直线平行,同旁内角互补解答.

练习册系列答案
相关题目
2.扇形周长为1,当扇形的半径为R时,扇形有最大面积S,则R和S的值为( )
| A. | $\frac{1}{4}$,$\frac{1}{16}$ | B. | $\frac{1}{2}$,$\frac{1}{8}$ | C. | $\frac{1}{4}$,$\frac{1}{8}$ | D. | $\frac{1}{2}$,$\frac{1}{16}$ |
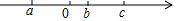 已知有理数a、b、c在数轴上的位置如图所示:化简:2(a+b)-3|a-c|+2|c-b|
已知有理数a、b、c在数轴上的位置如图所示:化简:2(a+b)-3|a-c|+2|c-b|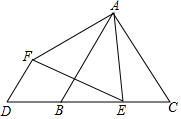 如图,点D在等边△ABC边CB的延长线上,点E是边BC上的动点,连结AE,在AE的左侧构造等边△AEF,连结DF,若DB=2,则DF的最小值是$\sqrt{3}$.
如图,点D在等边△ABC边CB的延长线上,点E是边BC上的动点,连结AE,在AE的左侧构造等边△AEF,连结DF,若DB=2,则DF的最小值是$\sqrt{3}$.